蒟阵P3390 【模板】矩阵快速幂

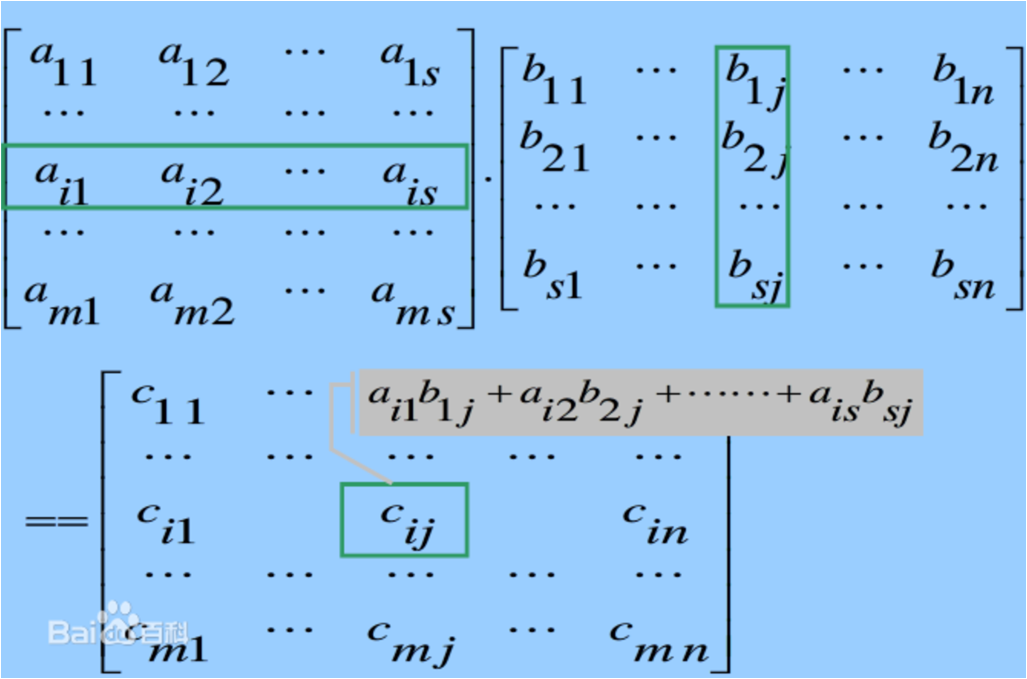
代码如下：

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<cmath>
 #include<cstring>
 #include<string>
 #include<algorithm>
 #include<time.h>
 using namespace std;
 #define mod 1000000007
 #define ll long long
 ll read(){
     ll ans=;
     char last=' ',ch=getchar();
     while(ch<'' || ch>'')last=ch,ch=getchar();
     while(ch>='' && ch<='')ans=ans*+ch-'',ch=getchar();
     if(last=='-')ans=-ans;
     return ans;
 }//快读
 struct matrix{
     ll m[][];
 };//定义蒟阵
 ll n,k;
 matrix a,c,e;
 matrix cheng(matrix x,matrix y)//定义蒟阵乘法
 {
     matrix c;
     for(ll i=;i<=n;i++)
         for(ll j=;j<=n;j++)
             c.m[i][j]=;//初始化0
     for(int i=;i<=n;i++)
       for(int j=;j<=n;j++)
         for(int k=;k<=n;k++)
         {
             c.m[i][j]=c.m[i][j]%mod+x.m[i][k]*y.m[k][j]%mod;//按照定义计算喽
         }
     return c;
 }
 matrix pow(matrix x,ll y)//定义蒟阵快速幂(注意要用蒟阵的乘法，其他相同)
 {
     matrix ans=e;
     while(y)
     {
         if(y&)
         {
             ans=cheng(ans,x);
         }
         x=cheng(x,x);
         y>>=;
     }
     return ans;
 }
 int main()
 {
     n=read(),k=read();
     for(ll i=;i<=n;i++)
         e.m[i][i]=;//单位蒟阵
     for(ll i=;i<=n;i++)
         for(ll j=;j<=n;j++)
         {
             a.m[i][j]=read();//读入
         }
     matrix ans=pow(a,k);
     for(ll i=;i<=n;i++)
     {
         for(ll j=;j<=n;j++)
         {
             cout<<ans.m[i][j]%mod<<" ";
         }
         cout<<endl;
     }
     return ;//结束喽
 }

如果要写蒟阵乘法的话，稍微修改一下就可以了：

int main()
{
    for(int i=;i<=m;i++)
        for(int j=;i<=n;j++)
        {
            c[i][j]=;
            for(int k=;i<=p;k++)
                c[i][j]+=a[i][k]*b[k][j];
        }
 }