牛客网多校第4场 A.Ternary String 【欧拉降幂】

题目：戳这里

学习博客：戳这里

欧拉函数的性质：

① N是不为0的整数。φ(1)=1（唯一和1互质的数就是1本身）

② 除了N=2,φ(N)都是偶数.

③ 小于N且与N互质的所有数的和是φ(n)*n/2。

④ 欧拉函数是积性函数——若m,n互质，φ(m*n)=φ(m)*φ(n)。

⑤ 当N为奇数时，φ(2*N)=φ(N)

⑥ 若N是质数p的k次幂，φ(N)=p^k-p^(k-1)=(p-1)p^(k-1)，因为除了p的倍数外，其他数都跟N互质。

⑦ 当N是质数时，φ(N) = N-1

广义欧拉定理：

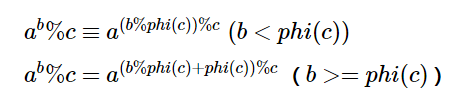
题意和解题思路见上面的学习博客

重点图：

 

通过这题的计算我们可以发现，对于任何模的欧拉降幂都是可以直接预处理的。

因为phi(1) = 1，而1e9 + 7递归求的phi才28个。

  1 #include<iostream>
  2 #include<algorithm>
  3 #include<stdio.h>
  4 #include<string.h>
  5 #include<string>
  6 #include <cmath>
  7 using namespace std;
  8 typedef long long ll;
  9 const ll mod = 1e9 + 7;
 10 const int maxn = 2e5 + 10;
 11 char s[maxn];
 12 ll qmul(ll a, ll b, ll m)
 13 {
 14     ll ans = 0;
 15     while(b)
 16     {
 17         if(b & 1)
 18             ans = (ans + a) % m;
 19         b >>= 1;
 20         a = (a + a) % m;
 21     }
 22     return ans;
 23 }
 24 ll qmod(ll a, ll b, ll m)
 25 {
 26     ll ans = 1;
 27     while(b)
 28     {
 29         if(b & 1)
 30             ans = qmul(ans, a, m) % m;
 31         b >>= 1;
 32         a = qmul(a, a, m) %m;
 33     }
 34     return ans;
 35 }
 36 ll phi(ll x)
 37 {
 38     ll i, res = x;
 39     for(i = 2; i < sqrt(x * 1.0) + 1; ++i)
 40     {
 41         if(!(x % i))
 42         {
 43             res = res / i * (i - 1);
 44             while(!(x % i))
 45             {
 46                 x /= i;
 47             }
 48         }
 49     }
 50     if(x > 1)
 51         res = res / x * (x - 1);
 52     return res;
 53 }
 54 ll p[33];
 55 int main()
 56 {
 57     p[0] = p[1] = mod;
 58     int cnt = 0;
 59     for(int i = 2;; ++i)
 60     {
 61         p[i] = phi(p[i - 1]);
 62         if(p[i] == 1)
 63         {
 64             cnt = i;
 65             break;
 66         }
 67     }
 68     int t;
 69     scanf("%d", &t);
 70     while(t--)
 71     {
 72         int n;
 73         scanf("%s", s);
 74         n = strlen(s);
 75         int num = 0;
 76         int pos = 0;
 77         for(int i = n - 1; i >= 0; --i)
 78         {
 79             if(s[i] == '2')
 80                 ++num;
 81             if(num == 28)
 82             {
 83                 pos = i;
 84                 break;
 85             }
 86
 87         }
 88         ll ans = 0;
 89         ++num;
 90         for(int i = pos; i < n; ++i)
 91         {
 92             if(s[i] == '0')
 93                 ans = (ans + 1) % p[num];
 94             if(s[i] == '1')
 95                 ans = (2 * ans % p[num] + 2 % p[num]) % p[num];
 96             if(s[i] == '2')
 97             {
 98                 --num;
 99                 ans = (3 % p[num] * qmod(2, ans + 1, p[num])) % p[num];
100                 ans = (ans % p[num] - 3 + p[num]) % p[num];
101             }
102         }
103         printf("%lld\n", ans % mod);
104     }
105
106 }