【每日一题】【BFS&Lambda&重建二叉树】2022年2月15日-根据先序中序重建并输出二叉树的右视图

描述

请根据二叉树的前序遍历，中序遍历恢复二叉树，并打印出二叉树的右视图

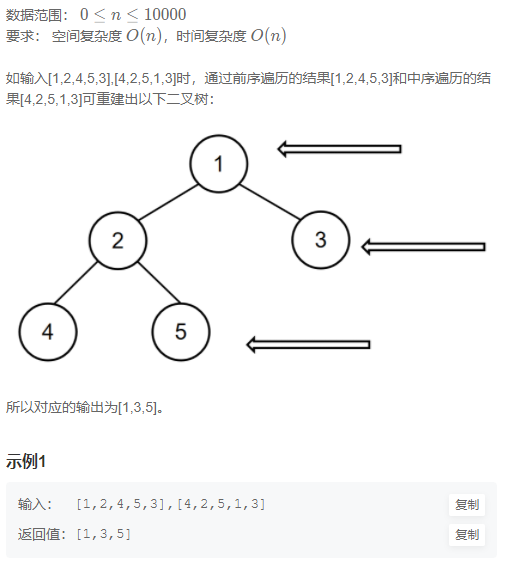
思路：重建&层次遍历记录最后一个&Lambda表达式

答案：

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 求二叉树的右视图
     * @param xianxu int整型一维数组 先序遍历
     * @param zhongxu int整型一维数组 中序遍历
     * @return int整型一维数组
     */
    //思路：使用队列BFS层次遍历，当到达最后一个节点时加入res
    public int[] solve (int[] xianxu, int[] zhongxu) {
        List<Integer> res = new ArrayList<>();
        //先确定二叉树
        TreeNode root = reconstrution(xianxu, 0, xianxu.length - 1, zhongxu, 0, zhongxu.length - 1);
        //使用队列，对树进行层次遍历
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()) {
            int size = queue.size();
            for(int i = 0; i < size; i++) {
                if(i == size - 1) {
                    res.add(queue.peek().val);
                }
                TreeNode node = queue.poll();
                if(node.left != null) {
                    queue.offer(node.left);
                }
                if(node.right != null) {
                    queue.offer(node.right);
                }
            }
        }
        return res.stream().mapToInt(x -> x).toArray();
    }
    //递归，类似回溯：路径、选择列表、结束条件
    //但是回溯要移除选择，而递归无需移除选择
    public TreeNode reconstrution(int[] xianxu, int preStart, int preEnd, int[] zhongxu, int inStart, int inEnd) {
        if(preStart > preEnd || inStart > inEnd) {
            return null;
        }
        TreeNode root = new TreeNode(xianxu[preStart]);
        //找到中序的位置
        int i = 0;
        for(i = inStart; i <= inEnd; i++) {
            if(zhongxu[i] == xianxu[preStart]) {
                break;
            }
        }
        root.left = reconstrution(xianxu, preStart + 1, preStart + (i - inStart), zhongxu, inStart, i - 1);
        root.right = reconstrution(xianxu, preStart + (i - inStart) + 1, preEnd, zhongxu, i + 1, inEnd);
        return root;
    }
}