LeetCode 题解 | 面试题57 - II. 和为s的连续正数序列

题目描述

面试题57 - II. 和为s的连续正数序列

难度简单37收藏分享切换为英文关注反馈

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。

序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

示例 1：

输入：target = 9
输出：[[2,3,4],[4,5]]

示例 2：

输入：target = 15
输出：[[1,2,3,4,5],[4,5,6],[7,8]]

限制：

• 1 <= target <= 10^5

方法一：

0ms 9.1MB都击败100%C++

class Solution {
public:
    vector<vector<int>> findContinuousSequence(int target) {
        vector<vector<int>>res;
        int i=1;
        while(target>0){
            target-=i++;
            if(target>0&&target%i==0){
                vector<int>tmp;
                for(int j=0;j<i;++j)tmp.emplace_back(target/i+j);
                res.emplace_back(tmp);
            }
        }
        reverse(res.begin(),res.end());
        return res;
    }
};

方法二：滑动窗口

什么是滑动窗口

滑动窗口可以看成数组中框起来的一个部分。在一些数组类题目中，我们可以用滑动窗口来观察可能的候选结果。当滑动窗口从数组的左边滑到了右边，我们就可以从所有的候选结果中找到最优的结果。

对于这道题来说，数组就是正整数序列$ [1, 2, 3, \dots, n]$。我们设滑动窗口的左边界为 ii，右边界为 jj，则滑动窗口框起来的是一个左闭右开区间 \([i, j)\)。注意，为了编程的方便，滑动窗口一般表示成一个左闭右开区间。在一开始，\(i=1, j=1i=1,j=1\)，滑动窗口位于序列的最左侧，窗口 大小为零。

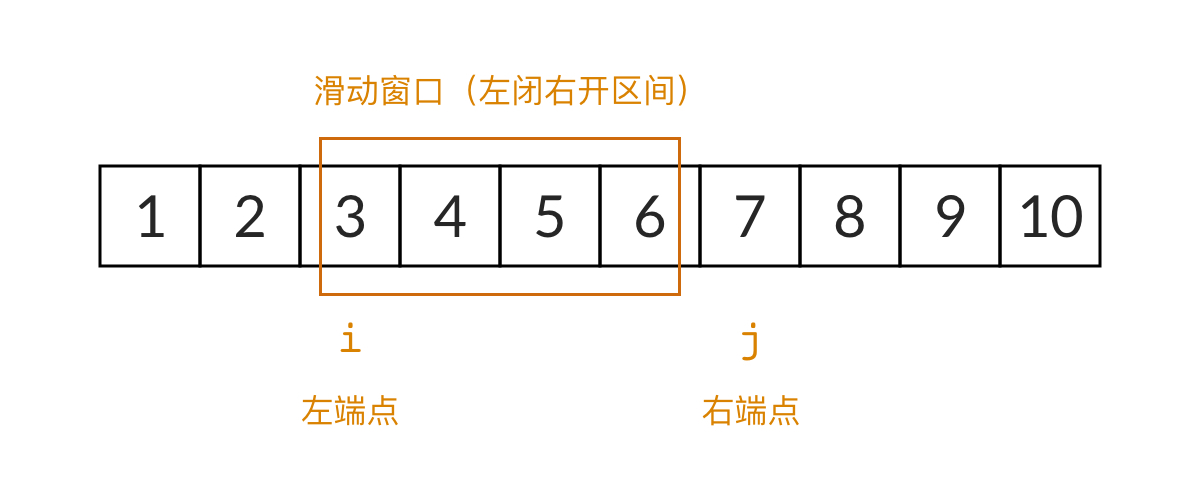
滑动窗口的重要性质是：窗口的左边界和右边界永远只能向右移动，而不能向左移动。这是为了保证滑动窗口的时间复杂度是 \(O(n)\)。如果左右边界向左移动的话，这叫做“回溯”，算法的时间复杂度就可能不止 \(O(n)\)。

在这道题中，我们关注的是滑动窗口中所有数的和。当滑动窗口的右边界向右移动时，也就是 j = j + 1，窗口中多了一个数字 j，窗口的和也就要加上 j。当滑动窗口的左边界向右移动时，也就是 i = i + 1，窗口中少了一个数字 i，窗口的和也就要减去 i。滑动窗口只有 右边界向右移动（扩大窗口） 和 左边界向右移动（缩小窗口） 两个操作，所以实际上非常简单。

如何用滑动窗口解这道题

要用滑动窗口解这道题，我们要回答两个问题：

第一个问题，窗口何时扩大，何时缩小？

第二个问题，滑动窗口能找到全部的解吗？

对于第一个问题，回答非常简单：

当窗口的和小于target的时候，窗口的和需要增加，所以要扩大窗口，窗口的右边界向右移动

当窗口的和大于 target 的时候，窗口的和需要减少，所以要缩小窗口，窗口的左边界向右移动

当窗口的和恰好等于 target 的时候，我们需要记录此时的结果。设此时的窗口为$ [i, j)$，那么我们已经找到了一个 $i \(开头的序列，也是唯一一个 ii 开头的序列，接下来需要找\)i+1$ 开头的序列，所以窗口的左边界要向右移动

对于第二个问题，我们可以稍微简单地证明一下：

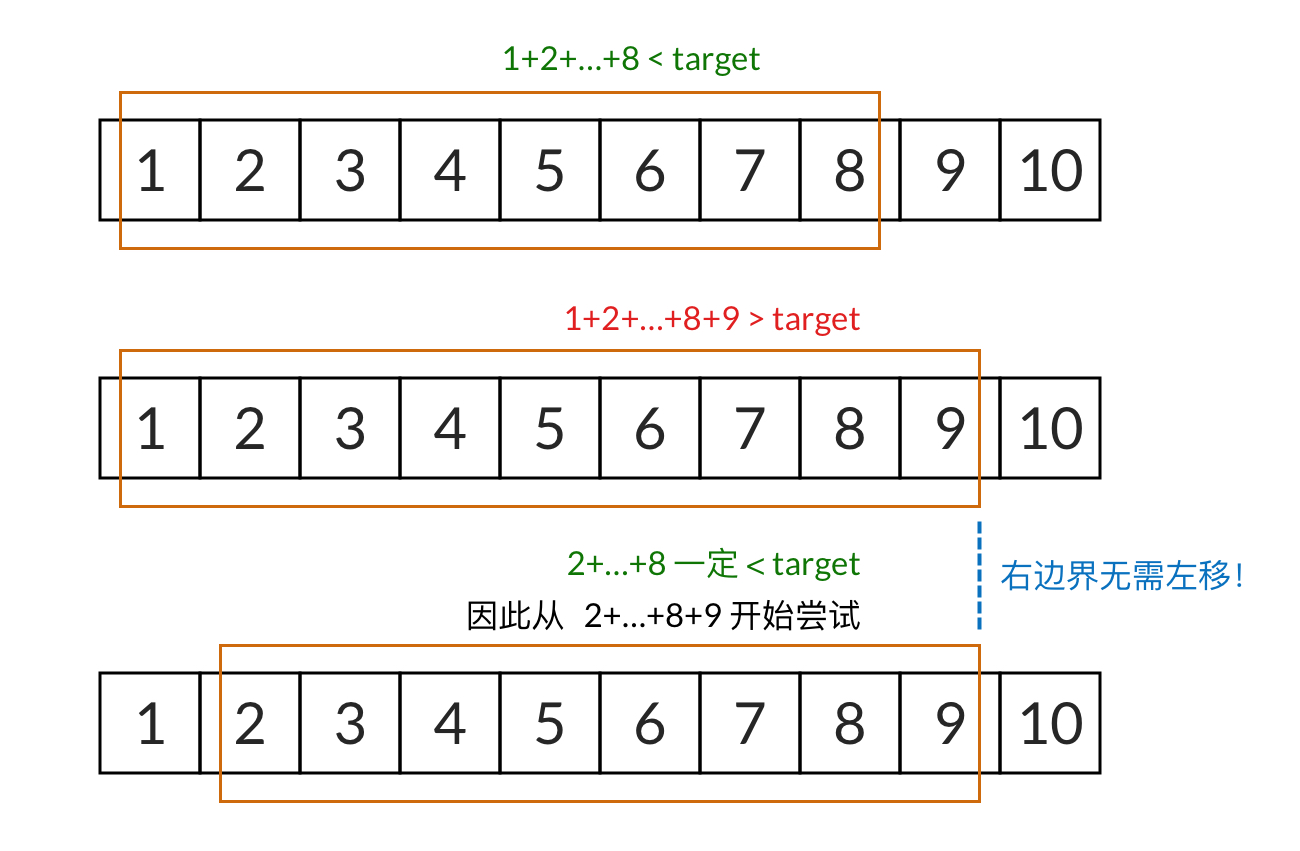
我们一开始要找的是 1 开头的序列，只要窗口的和小于 target，窗口的右边界会一直向右移动。假设$ 1+2+\dots+81+2+⋯+8 小于 target$，再加上一个 9 之后， 发现 \(1+2+\dots+8+91+2+⋯+8+9\) 又大于target了。这说明 1 开头的序列找不到解。此时滑动窗口的最右元素是$ 9$。

接下来，我们需要找 2 开头的序列，我们发现，\(2 + \dots + 8 < 1 + 2 + \dots + 8 < \mathrm{target}2+⋯+8<1+2+⋯+8<target\)。这说明$ 2$ 开头的序列至少要加到$ 9$。那么，我们只需要把原先 \(1~9\) 的滑动窗口的左边界向右移动，变成$ 2~9 $的滑动窗口，然后继续寻找。而右边界完全不需要向左移动。

以此类推，滑动窗口的左右边界都不需要向左移动，所以这道题用滑动窗口一定可以得到所有的解。时间复杂度是$ O(n)$。

注：这道题当前可以用等差数列的求和公式来计算滑动窗口的和。不过我这里没有使用求和公式，是为了展示更通用的解题思路。实际上，把题目中的正整数序列换成任意的递增整数序列，这个方法都可以解。

资料出自nettee

8ms 9.1MB

vector<vector<int>> findContinuousSequence(int target) {
    int i = 1; // 滑动窗口的左边界
    int j = 1; // 滑动窗口的右边界
    int sum = 0; // 滑动窗口中数字的和
    vector<vector<int>> res;

    while (i <= target / 2) {
        if (sum < target) {
            // 右边界向右移动
            sum += j;
            j++;
        } else if (sum > target) {
            // 左边界向右移动
            sum -= i;
            i++;
        } else {
            // 记录结果
            vector<int> arr;
            for (int k = i; k < j; k++) {
                arr.push_back(k);
            }
            res.push_back(arr);
            // 左边界向右移动
            sum -= i;
            i++;
        }
    }

    return res;
}