【Aizu - 0189】Convenient Location （最短路 Floyd算法）

Convenient Location

直接翻译了

Descriptions

明年毕业的A为就业而搬家。就职的公司在若干城市都有办公室，不同天出勤的办公室也不同。所以A在考虑住在哪去各个办公室的时长最短。

你为了帮助A，决定去找最方便的居住城市。

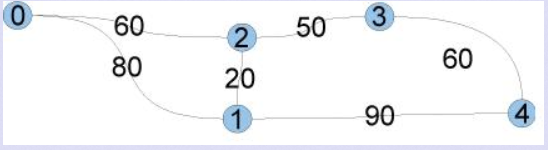
城市从0号开始编号，城市之间有道路。不同的道路对应着不同的通勤时间。A 从所住的城市到该城市的办公室的通勤时间认为是 0。此时考虑到所有城市的通勤时间。例如，城市和道路的设置如图所示，A 住在城市 1 的情形下，到不同城市的通勤时间是

到城市 0：80
到城市 1：0
到城市 2：20
到城市 3：70
到城市 4：90

总和为 260。

输入道路的数量和所有道路的信息，求出到所有城市的通勤时间最小值和这个最小值对应的城市编号。若有多个城市的总通勤时间都是最小值，输出这些城市编号中的最小值。城市的总数不超过 10，道路的总数不超过 45，所有道路都是双向的，且两个方向的通勤时间是相等的。每个城市到其他任一城市都存在道路。

Input

有多组测试数据，输入由单行 0 终止。每个测试数据格式如下。

n
a1 b1 c1
a2 b2 c2
:
an bn cn

第1行给出道路数目 n (1 ≤ n ≤ 45) 。接下来 n 行给出第 i 个道路的信息。 a_i, b_i (0 ≤ a_i, b_i ≤ 9) 是第 i 个道路连接的城市的编号，c_i (0 ≤ c_i ≤ 100) 是这条道路的通勤时间。

Output

对每个测试数据，输出总通勤时间的最小值和对应最小的城市编号，由空格分开，结尾是换行符。

Sample Input

6
0 1 80
1 2 20
0 2 60
2 3 50
3 4 60
1 4 90
2
0 1 1
1 2 1
0

Output for the Sample Input

2 240
1 2

题目链接

https://vjudge.net/problem/Aizu-0189

经典Floyd算法求最短路，模板题，没啥说的

AC代码

#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
#include <sstream>
#define IOS ios_base::sync_with_stdio(0); cin.tie(0)
#define Mod 1000000007
#define eps 1e-6
#define ll long long
#define INF 0x3f3f3f3f
#define MEM(x,y) memset(x,y,sizeof(x))
#define Maxn 50
#define P pair<int,int>
using namespace std;
int n;
int maxx;//编号最大的城市为maxx
int d[Maxn][Maxn];//d[i][j]从i到j的最短距离
//Floyd算法求各个城市之间的最短距离
void Floyd()
{
    for(int k=; k<=maxx;k++)
        for(int i=;i<=maxx;i++)
            for(int j=;j<=maxx;j++)
                d[i][j]=min(d[i][k]+d[k][j],d[i][j]);
}
int main()
{
    IOS;
    while(cin>>n,n)
    {
        MEM(d,INF);//初始化城市距离，两两之间的距离为无穷大
        for(int i=;i<=n;i++)
            d[i][i]=;//i到i的距离为0
        maxx=-;
        while(n--)
        {
            int a,b,c;
            cin>>a>>b>>c;
            maxx=max(maxx,max(a,b));
            d[a][b]=d[b][a]=c;
        }
        Floyd();//求最短距离
        int ans=INF;//总距离
        int pos;//编号为pos的城市
        for(int i=;i<=maxx;i++)//枚举i到各个城市之间的距离
        {
            int sum=;
            for(int j=;j<=maxx;j++)
                sum+=d[i][j];
            if(ans>sum)
            {
                ans=sum;
                pos=i;
            }
        }
        cout<<pos<<" "<<ans<<endl;
    }
    return ;
}