纪中5日T2 1565. 神秘山庄

1565. 神秘山庄 (Standard IO)

原题

题目描述

翠亨村是一个神秘的山庄，并不是因为它孕育了伟人孙中山，更神秘的是山庄里有N只鬼、M只兔子，当然还有你。其中每秒钟：

1. 恰有两个生物遇到。

2. 任意两个生物之间相遇的概率是均等的。

如果两只兔子相遇，没有事情发生；如果两只鬼相遇，他们会互相厮打，最终一起死亡；如果鬼遇到兔子，兔子就会被吃掉；如果鬼遇到你，哈哈。。。。symbol就见不到你了；如果你遇到兔子，那么你可以选择杀或不杀(概率相等)。

问你能活着见symbol的概率。

 

输入

第一行两个整数N,M。

输出

一个实数，表示你活下来的概率，精确到小数点后6位。

 

样例输入

0 0

样例输出

1.000000

 

数据范围限制

 

 

提示

【限制】

0<=N,M<=1000。

对于20%的数据：N,M<=10。

对于30%的数据：M=0。

Solution

首先我们要明确是无限的时间。你想活下来，只能要鬼鬼们自相残杀。

兔子

兔子就是来耗时间的，这与存活概率无关。

那么我们就无视M，只考虑N。

鬼

要是有奇数只鬼，

你再怎么挣扎，

最后一定回剩一只来打你

你必死无疑。

要是有偶数只鬼，

（emm……貌似不好直接算）

如果有两只鬼

　　以其中一只鬼鬼的视角：

　　要么遇到你，要么遇到另一只鬼鬼。

　　所以概率就是0.500000（1/2）

如果有n只鬼

　　把鬼鬼们和你并排放在一起，并且两两配对

　　由于有n+1个物体，所以总是会剩下一个物体

　　这个物体可能是你，也可能是我鬼。

　　剩下的是一号鬼鬼的概率是1/（n+1）

　　　　是三号鬼鬼的概率也是1/（n+1）

　　那么剩下你的概率也还是1/（n+1）

所以说

最终概率即为：

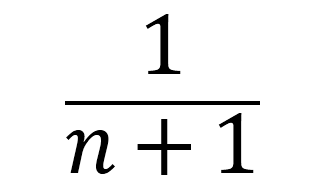
Code

 #include<bits/stdc++.h>
 using namespace std;
 int n,m;
 double gl=1.0;//别忘记初始化为1.0！
 int main()
 {
     cin>>n>>m;//n是鬼
     if(n%==)
         gl=0.00000;
     else
     gl=/((n+)*1.0);
     printf("%.6lf",gl);
     return ;
 }

Summary

有些题目，看不出来是什么模型，只能先模拟的，不妨先想想数论吧！

不要因为电脑在面前，就不愿意动笔了！