A novel multi-swarm particle swarm optimization with dynamic learning strategy(一种新颖的具有动态学习策略的多种群粒子群优化算法)

1、核心

• 在每个子种群的粒子被划分为普通粒子（ordinary particles）和交流粒子（communication particles），在每次迭代过程中，不同的粒子执行不同的进化操作。普通粒子用于探索能力（exploitation），交流粒子用于开发能力（exploration）。
• 设置一个动态的逐渐增加的控制参数p，用于实现分类操作，即将粒子分为普通粒子和交流粒子，同时，使普通粒子逐渐进化为交流粒子。

2、相关描述

• 将初始种群（original population）划分为M*N个粒子（M为子种群数量，N为每个子种群的粒子数）。
• 将每个子种群中的最佳粒子（best particle）被当做 lbest. 通过公式（3）来指导每个子种群中的粒子（普通粒子，implemented as a probability 1 − p）的进化。

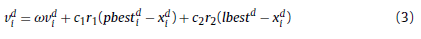
• 对于每个子种群中的交流粒子，以概率p 通过公式（4）执行粒子的进化。

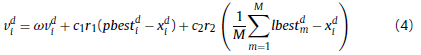
其中，lbest_m表示到目前为止在每个子种群中发现的最佳粒子的位置，m=[1,2,...,M]。

• 图1清楚的解释了提出的具有动态学习策略的多种群粒子群算法的概念。

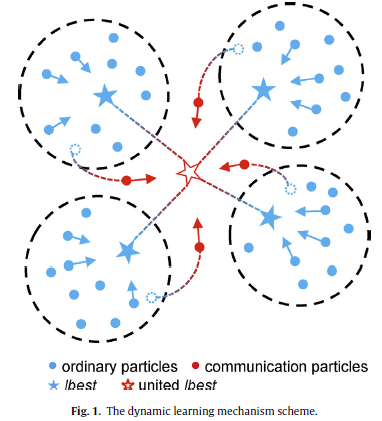
• 位置更新公式通过公式（2）执行。

　　

3、算法伪代码