C# 逆变与协变

该文章中使用了较多的 委托delegate和Lambda表达式，如果你并不熟悉这些，请查看我的文章《委托与匿名委托》、《匿名委托与Lambda表达式》以便帮你建立完整的知识体系。

在C#从诞生到发展壮大的过程中，新知识点不断引入。逆变与协变并不是C#独创的，属于后续引入。在Java中同样存在逆变与协变，后续我还会写一篇Java逆变协变的文章，有兴趣的朋友可以关注一下。

逆变与协变，听起来很抽象、高深，其实很简单。看下面的代码：

class Person
    {

    }
    class Student : Person
    {

    }
    class Teacher: Person
    {

    }

    class Program
    {
        static void Main(string[] args)
        {
            List<Person> plist = new List<Person>();
            plist = new List<Student>();
            plist = new List<Teacher>();
}
}

在上面的代码中，plist = new List<Student>()、plist = new List<Teacher>()两句产生编译错误。虽然Person是Student/Teacher的父类，但List<Person>类型却不是List<Student/Teacher>类型的父类，所以上面的赋值语句报类型转换失败错误。

如上这样的赋值操作，在C# 4.0之前是不允许的，至于为什么不允许，类型安全是首要因素。看下面的示例代码：

List<Person> plist = new List<Student>();
plist.Add(new Person());
plist.Add(new Student());
plist.Add(new Teacher());

如下示例，假设 List<Person> plist = new List<Student>() 允许赋值，那plist虽然类型为List<Person>集合，但实际指向确是List<Student>集合。plist.Add(new Person())，添加操作实际调用的是List<Student>.Add()。Person类型无法安全转换为Student，所以这样的集合定义没有意义，所以上面的假设不成立。

但情况在C# 4.0之后发生了变化，并不是"不可能发生的事情发生了"，而是应用的灵活性做出了新的调整。同样的在C# 4.0中上面的程序仍是不被允许的，但却出现了例外。从C# 4.0开始，在泛型委托、泛型接口中，允许特殊情况的发生（实质上并未发生特殊变化，后面说明）。如下示例：

delegate void Work<T>(T item);

class Person
{
        public string Name { get; set; }
}
class Student : Person
{
        public string Like { get; set; }
}
class Teacher : Person
{
        public string Teach { get; set; }
}

class Program
{
        static void Main(string[] args)
        {
            Work<Person> worker = (p) => { Console.WriteLine(p.Name); }; ;
            Work<Student> student_worker = (s) => { Console.WriteLine(s.Like); };
            student_worker = worker; //此处编译错误
        }
}

根据前面的理论支持，student_worker = worker;的错误很容易理解。但此处我们程序的目的是让 woker  充当 Work<Student> 的功能，以后调用 student_worker(s)实际调用的是woker(s)。为了满足我们的需求，需要程序做2方面的处理：

1、因在调用student_worker(s)时，实质执行的是woker(s)，所以需要s变量的类型能成功转换为woker需要的参数类型。

2、需要告诉编译器，此处允许将 Work<Person> 类型的对象赋值给 Work<Student>类型的变量。

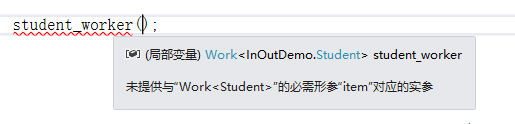
条件1在调用时student_worker()，时编译器会提示要求参数必须是Student类型对象，该对象可成功转换为Person类型对象。

条件2则需要对Woke委托定义进行调整，调整如下：

delegate void WorkIn<in T>(T item);

委托名字改为WorkIn是为却别修改前后的委托，关键之处为<in T>。通过增加 in 关键字，标注该泛型委托的类型参数T，仅作为委托方法的参数来使用。此时上面的程序便可成功编译并执行。

delegate void WorkIn<in T>(T item);
class Program
    {
        static void Main(string[] args)
        {
            WorkIn<Person> woker = (p) => { Console.WriteLine(p.Name); };
            WorkIn<Student> student_worker = woker;
            student_worker(new Student() { Name="tom", Like="C#" });

        }
    }

对于要求类型参数为子类型，允许赋值类型参数为父类型值的这种情况，称为逆变。逆变在C#中需要用 in 标注泛型的类型参数。逆变虽叫逆变，但只是形式上看似父类对象赋值给子类变量，实质上是方法调用时参数的类型转换。Student s = new Person()，这是不可能的，这不是逆变是错误。

上面的代码如你能转换为下面的形式，那你就可以忘却逆变，本质比现象更重要