Stanford机器学习---第九讲. 聚类

原文：http://blog.csdn.net/abcjennifer/article/details/7914952

本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。内容大多来自Standford公开课machine learning中Andrew老师的讲解和其他书籍的借鉴。（https://class.coursera.org/ml/class/index）

第九讲. 聚类——Clustering

 

===============================

（一）、什么是无监督学习？

（二）、KMeans聚类算法

（三）、Cluster问题的(distortion)cost function

（四）、如何选择初始化时的类中心

（五）、聚类个数的选择

=====================================

（一）、什么是无监督学习

之前的几章我们只涉及到有监督学习，本章中，我们通过讨论另一种Machine learning方式：无监督学习。首先呢，我们来看一下有监督学习与无监督学习的区别。

给定一组数据(input，target)为Z=(X，Y)。

有监督学习：最常见的是regression & classification。

• regression：Y是实数vector。回归问题，就是拟合(X，Y)的一条曲线，使得下式cost function L最小。

• classification：Y是一个finite number，可以看做类标号。分类问题需要首先给定有label的数据训练分类器，故属于有监督学习过程。分类问题中，cost function L(X,Y)是X属于类Y的概率的负对数。

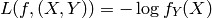，其中f_i(X)=P(Y=i | X);

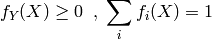
无监督学习：无监督学习的目的是学习一个function f，使它可以描述给定数据的位置分布P(Z)。 包括两种：density estimation & clustering.

• density estimation就是密度估计，估计该数据在任意位置的分布密度
• clustering就是聚类，将Z聚集几类（如K-Means），或者给出一个样本属于每一类的概率。由于不需要事先根据训练数据去train聚类器，故属于无监督学习。
• PCA和很多deep learning算法都属于无监督学习。

好了，大家理解了吧，unsupervised learning也就是不带类标号的机器学习。

练习：

=====================================

（二）、K-Means聚类算法

KMeans是聚类算法的一种，先来直观的看一下该算法是怎样聚类的。给定一组数据如下图所示，K-Means算法的聚类流程如图：

图中显示了Kmeans聚类过程，给定一组输入数据{x(1),x(2),...,x(n)}和预分类数k，算法如下：

首先随机指定k个类的中心U1~Uk，然后迭代地更新该centroid。

其中，C(i)表示第i个数据离那个类中心最近，也就是将其判定为属于那个类，然后将这k各类的中心分别更新为所有属于这个类的数据的平均值。

=====================================

（三）、Cluster问题的(distortion)cost function

在supervised learning中我们曾讲过cost function，类似的，在K-means算法中同样有cost function，我们有时称其为distortion cost function.

如下图所示，J(C,U)就是我们要minimize的function.

即最小化所有数据与其聚类中心的欧氏距离和。

再看上一节中我们讲过的KMeans算法流程，第一步为固定类中心U，优化C的过程：

第二步为优化U的过程：

这样进行迭代，就可以完成cost function J的优化。

练习：

这里大家注意，回归问题中有可能因为学习率设置过大产生随着迭代次数增加，cost function反倒增大的情况。但聚类是不会产生这样的问题的，因为每一次聚类都保证了使J下降，且无学习率做参数。

=====================================

（四）、如何选择初始化时的类中心

在上面的kmeans算法中，我们提到可以用randomly的方法选择类中心，然而有时效果并不是非常好，如下图所示：

fig.1. original data

对于上图的这样一组数据，如果我们幸运地初始化类中心如图2，

fig.2. lucky initialization

fig.3. unfortunate initialization

但如果将数据初始化中心选择如图3中的两种情况，就悲剧了！最后的聚类结果cost function也会比较大。针对这个问题，我们提出的solution是，进行不同initialization（50~1000次），每一种initialization的情况分别进行聚类，最后选取cost function J(C,U)最小的作为聚类结果。

 

=====================================

（五）、聚类个数的选择

How to choose the number of clusters? 这应该是聚类问题中一个头疼的part，比如KMeans算法中K的选择。本节就来解决这个问题。

最著名的一个方法就是elbow-method，做图k-J(cost function)如下：

若做出的图如上面左图所示，那么我们就找图中的elbow位置作为k的选定值，如果像右图所示并无明显的elbow点呢，大概就是下图所示的数据分布：

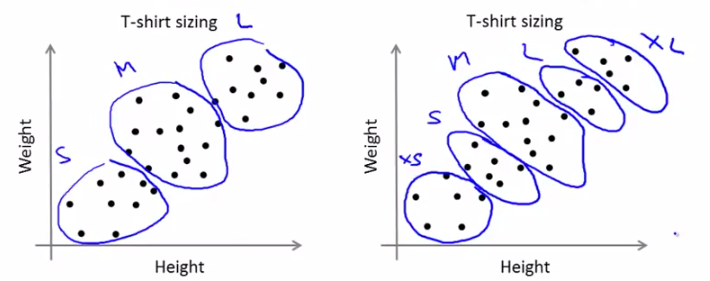
这种情况下需要我们根据自己的需求来进行聚类，比如Tshirt的size，可以聚成{L,M,S}三类，也可以分为{XL，L，M，S，XS}5类。需要大家具体情况具体分析了~

练习：

==============================================

小结

 

本章讲述了Machine learning中的又一大分支——无监督学习，其实大家对无监督学习中的clustering问题应该很熟悉了，本章中讲到了几个significant points就是elbow 方法应对聚类个数的选择和聚类中心初始化方法，值得大家投入以后的应用。