FHQ treap(无旋treap)

平衡树

• 平衡树作为一种中级数据结构，有着广泛的使用场景。其平衡性的维护方式灵活多变，而其中的无旋treap更以简单著称

P3369 【模板】普通平衡树

• 题意：
  
  需维护以下操作：
  
  插入一个数 x。
  
  删除一个数 x（若有多个相同的数，应只删除一个）。
  
  定义排名为比当前数小的数的个数 +1。查询 x 的排名。
  
  查询数据结构中排名为 x 的数。
  
  求 x 的前驱（前驱定义为小于 x，且最大的数）。
  
  求 x 的后继（后继定义为大于 x，且最小的数）。
• 平衡树是一种二叉搜索树，而treap将其与堆结合，使其同时具有二者的性质。
  
  treap通过给每个节点一个随机数值，依靠这个值维护一个堆，保证树的平衡性。
  
  而无旋treap通过两种关键操作来维护这两者的性质：split和merge

split

• split将目标树按值分裂成两棵树，由于分裂后需要返回两颗树的根，不好返回，因此用指针&x和&y来传递分裂后的两个根
  
  由于二叉搜索树的性质：u左子树的节点值都比u的权值小，而右子树的都比u的大。因此如果分裂目标k比u小，那么就去左子树找
  
  反之亦然
  
  由于二叉搜索树的性质，分裂出来的x子树中的所有值都比y子树中的所有值小。这个性质在合并时非常关键
  
  代码：

#define ls (tr[u].l)
#define rs (tr[u].r)
void push_up(int u)
{
	tr[u].size=1+tr[ls].siz+tr[rs].siz;
}
void split(int u,int &x,int &y,int k)
{
	if(u==0){x=0,y=0;return;}
	if(tr[u].val<=k)
	{
		x=u,split(rs,rs,y,k);
	}
	else y=u,split(ls,x,ls,k);
	push_up(u);
}

容易理解，split并不破坏原treap堆的性质

• 注意 代码中关于&x与&y的确定需要特别强调。x代表分裂出来权值较小的子树的根节点,y代表分裂出来权值较大的子树的根节点，如下图
  
  
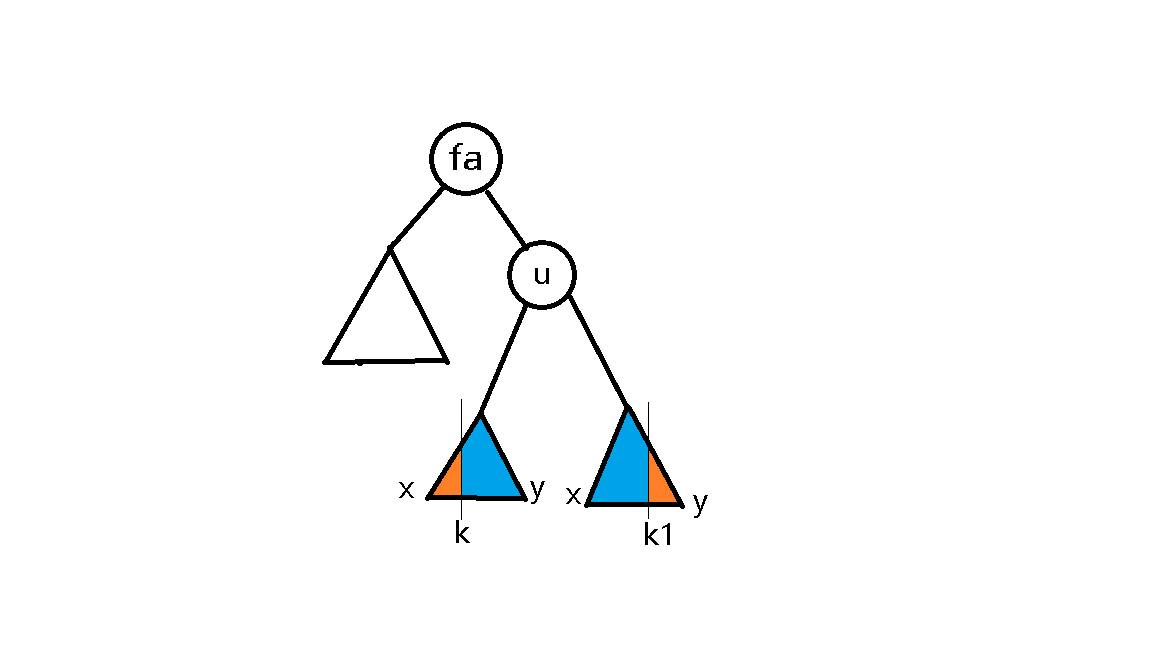
• 如果k比u的值大，证明整个左子树都比k小，因此这时的k就在k1的位置上。
  
  因此u及其子树k1左边的全是属于其父亲给出的x，即分裂出的较小的子树。而较大的子树还不知道，就到k1右边的橙色部分中找
  
  而将u的右子树带到split函数中x的位置，是为了更新u的右子树，在分裂完成后将剩下的小于k的部分接回u右子树的空缺
  
  这个过程中，左子树无影响。分裂完后，u的大小很可能改变，因此要push_up更新大小
  
  而k在图中左边的原理同理，不再赘述。

merge

• merge是将两个二叉平衡树合并的函数，要求以x为根的子树中所有元素都必须小于y子树中的元素。这个要求看似苛刻，但正好与split出来的子树的性质不谋而合。
• 由于合并的两棵树x中所有值都比y小，因此对于二叉搜索树的性质，只需要将大的树接在小的树右下角或者小的接在大的左下角就行了。
• merge的关键是一个随机值：\(tr[u].rnd\) 。还记得前文说到treap是二叉搜索树与堆的结合吗？split并不破坏堆的性质，而merge正好就根据初始所附的随机值来维护堆的性质。如何维护具体看代码

int merge(int x,int y) //返回的是两树合并后的根节点
{
	if(!x||!y) return x+y; //如果x或y中任意一一个为零，就直接以另一个为根
	if(tr[x].rnd<tr[y].rnd) //维护的是小根堆。若x的随机值比y的小，那么x就在y上面，x作为根被返回
	{
		tr[x].r=merge(tr[x].r,y);push_up(x);return x;
	}
	else
	{
		tr[y].l=merge(x,tr[y].l);push_up(y);return y;//否则y当根，注意merge中带入的第一棵树值都比第二颗小
	}
}

具体操作

• 讲了这么多，实际上与开头具体的操作关系并不大。现在，就看看如何用以上两个函数实现这些操作

1. 插入
   
   先新建一个节点，再按这个点的值进行分裂。这时，其中一个子树中所有值都小于等于新建节点的值。依次合并回去就好了

mt19937 myrand(time(0));
int newnode(int val)
{
	int u=++cnt;
	tr[u].siz=1,tr[u].val=val,tr[u].l=tr[u].r=0,tr[u].rnd=myrand();
	return u;
}
int u=newnode(x);//x是输入进来的权值
int lrt,rrt;
split(root,lrt,rrt,x);
root=merge(merge(lrt,u),rrt);//注意合并时都要给root重新赋值

1. 删除
   
   按x-1、x、x+1分裂成3个树，中间那个树所有权值都是x了。但注意不能将整个树全部扔掉。直接将中间树根节点的左右儿子合并即可。

int lr,mr,rr;
split(root,lr,rr,x-1);split(rr,mr,rr,x+1);
mr=merge(tr[mr].l,tr[mr].r);
root=merge(merge(lr,mr),rr);

1. 查找x的排名
   
   按x-1分裂，直接输出较小的树的siz即可

int lr,rr;
split(root,lr,rr,x-1);
printf("%d\n",tr[lr].siz+1);
root=merge(lr,rr);

1. 查找排名为x的数
   
   根据二叉搜索树的性质直接找

int kth(int u,int k)
{
	int lsiz=tr[ls].size;
	if(lsiz+1==k) return u;
	if(lsiz+1>k) return kth(ls,k);
	else return kth(rs,k-lsiz-1);
}
printf("%d\n",tr[kth(root,x)].val);

1. 求x的前驱
   
   仍然利用kth函数，将root按x-1分裂成两个树，再找较小子树中最大的数

int lr,rr;
split(root,lr,rr,x-1);
printf("%d\n",tr[kth(lr,tr[lr].siz)].val);
root=merge(lr,rr);

1. 求x的后继
   
   几乎同上，按x+1分裂，找较大子树中最小的数

int lr,rr;
split(root,lr,rr,x+1);
printf("%d\n",tr[kth(rr,1)].val);
root=merge(lr,rr);

• 以上，就是普通平衡树的全部操作。

P2042 [NOI2005] 维护数列

• 题意：
  
  需要对一个连续数列维护以下操作：
  
  区间插入
  
  区间删除
  
  区间修改
  
  区间翻转
  
  区间求和
  
  求当前数列最大字段和
• 普通平衡树是维护一个集合的信息，那平衡树能不能维护一个连续数列呢？答案是可以的
• 普通平衡树与数列平衡树最大的区别在于split。
• 由于普通平衡树维护的是集合，操作大都与值相关，因此是按值分裂的
  
  而数列平衡树维护的是连续的数列，因此不能按值分裂，必须按位置分裂