hiho47 : 拓扑排序·一

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

由于今天上课的老师讲的特别无聊，小Hi和小Ho偷偷地聊了起来。

小Ho：小Hi，你这学期有选什么课么？

小Hi：挺多的，比如XXX1,XXX2还有XXX3。本来想选YYY2的，但是好像没有先选过YYY1，不能选YYY2。

小Ho：先修课程真是个麻烦的东西呢。

小Hi：没错呢。好多课程都有先修课程，每次选课之前都得先查查有没有先修。教务公布的先修课程记录都是好多年前的，不但有重复的信息，好像很多都不正确了。

小Ho：课程太多了，教务也没法整理吧。他们也没法一个一个确认有没有写错。

小Hi：这不正是轮到小Ho你出马的时候了么！

小Ho：哎？？

我们都知道大学的课程是可以自己选择的，每一个学期可以自由选择打算学习的课程。唯一限制我们选课是一些课程之间的顺序关系：有的难度很大的课程可能会有一些前置课程的要求。比如课程A是课程B的前置课程，则要求先学习完A课程，才可以选择B课程。大学的教务收集了所有课程的顺序关系，但由于系统故障，可能有一些信息出现了错误。现在小Ho把信息都告诉你，请你帮小Ho判断一下这些信息是否有误。错误的信息主要是指出现了"课程A是课程B的前置课程，同时课程B也是课程A的前置课程"这样的情况。当然"课程A是课程B的前置课程，课程B是课程C的前置课程，课程C是课程A的前置课程"这类也是错误的。

提示：拓扑排序

输入

第1行：1个整数T，表示数据的组数T(1 <= T <= 5)
接下来T组数据按照以下格式：
第1行：2个整数，N,M。N表示课程总数量，课程编号为1..N。M表示顺序关系的数量。1 <= N <= 100,000. 1 <= M <= 500,000
第2..M+1行：每行2个整数，A,B。表示课程A是课程B的前置课程。

输出

第1..T行：每行1个字符串，若该组信息无误，输出"Correct"，若该组信息有误，输出"Wrong"。

样例输入

2
2 2
1 2
2 1
3 2
1 2
1 3

样例输出

Wrong
Correct

提示：拓扑排序

小Ho拿出纸笔边画边说道：如果把每一门课程看作一个点，那么顺序关系也就是一条有向边了。错误的情况也就是出现了环。我知道了！这次我们要做的是判定一个有向图是否有环。

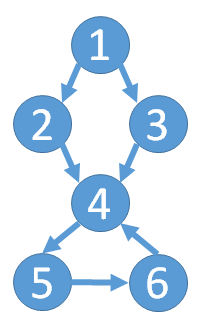
小Hi：小Ho你有什么想法么？

<小Ho思考了一会儿>

小Ho：一个直观的算法就是每次删除一个入度为0的点，直到没有入度为0的点为止。如果这时还有点没被删除，这些没被删除的点至少组成一个环；反之如果所有点都被删除了，则有向图中一定没有环。

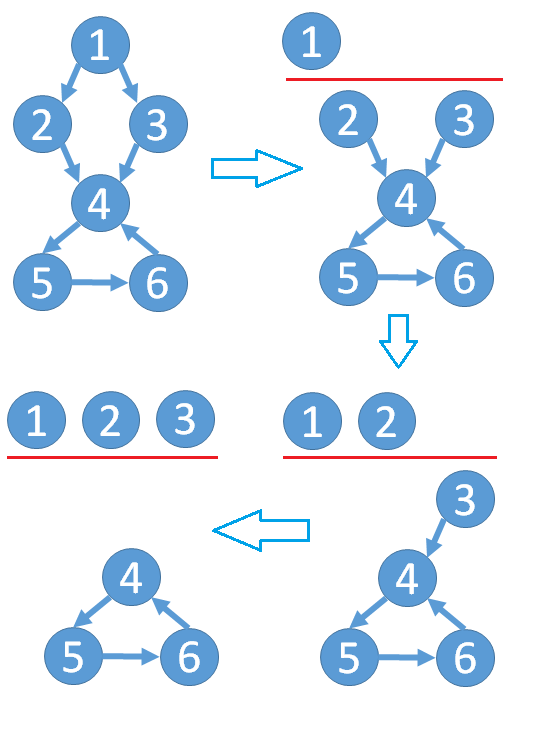
小Hi：Good Job！那赶快去写代码吧！

小Ho又思考了一会儿，挠了挠头说：每次删除一个点之后都要找出当前入度为0的点，这一步我没想到高效的方法。通过扫描一遍剩余的边可以找所有出当前入度为0的点，但是每次删除一个节点之后都扫描一遍的话复杂度很高。

小Hi赞许道：看来你已经养成写代码前分析复杂度的意识了！这里确实需要一些实现技巧，才能把复杂度降为O(N+M)，其中N和M分别代表点数和边数。我给你一个提示：如果我们能维护每个点的入度值，也就是在删除点的同时更新受影响的点的入度值，那么是不是就能快速找出入度为0的点了呢？

小Ho：我明白了，这个问题可以这样来解决：

1. 计算每一个点的入度值deg[i]，这一步需要扫描所有点和边，复杂度O(N+M)。

2. 把入度为0的点加入队列Q中，当然有可能存在多个入度为0的点，同时它们之间也不会存在连接关系，所以按照任意顺序加入Q都是可以的。

3. 从Q中取出一个点p。对于每一个未删除且与p相连的点q，deg[q] = deg[q] - 1；如果deg[q]==0，把q加入Q。

4. 不断重复第3步，直到Q为空。

最后剩下的未被删除的点，也就是组成环的点了。

小Hi：没错。这一过程就叫做拓扑排序。

小Ho：我懂了。我这就去实现它！

< 十分钟之后 >

小Ho：小Hi，不好了，我的程序写好之后编译就出诡异错误了！

小Hi：诡异错误？让我看看。

小Hi凑近电脑屏幕看了看小Ho的源代码，只见小Ho写了如下的代码：

int edge[ MAXN ][ MAXN ];

小Hi：小Ho，你有理解这题的数据范围么？

小Ho：N最大等于10万啊，怎么了？

小Hi：你的数组有10万乘上10万，也就是100亿了。算上一个int为4个字节，这也得400亿字节，将近40G了呢。

小Ho：啊？！那我应该怎么？QAQ

小Hi：这里就教你一个小技巧好了：

这道题目中N的数据范围在10万，若采用邻接矩阵的方式来储存数据显然是会内存溢出。而且每次枚举一个点时也可能会因为枚举过多无用的而导致超时。因此在这道题目中我们需要采用邻接表的方式来储存我们的数据：

常见的邻接表大多是使用的指针来进行元素的串联，其实我们可以通过数组来模拟这一过程。

int head[ MAXN + 1] = {0};	// 表示头指针，初始化为0
int p[ MAXM + 1];		// 表示指向的节点
int next[ MAXM + 1] = {0}; 	// 模拟指针，初始化为0
int edgecnt;			// 记录边的数量

void addedge(int u, int v) {	// 添加边(u,v)
	++edgecnt;
	p[ edgecnt ] = v;
	next[ edgecnt ] = head[u];
	head[u] = edgecnt;
}

// 枚举边的过程，u为起始点
for (int i = head[u]; i; i = next[i]) {
	v = p[i];
	...
}

小Ho：原来还有这种办法啊？好咧。我这就去改进我的算法=v=

 #include <iostream>
 #include <queue>
 #include <vector>
 using namespace std;

 bool isTuopu(vector<vector<int> >& Graph)  //拓扑排序
 {
     queue<int> Hq;    //记录入度为0的结点
     vector<int> rudu(Graph.size(), );  //记录结点的入度
     for(int i=; i<Graph.size(); i++)
     {
         for (int j=; j<Graph[i].size(); j++)
         {
             rudu[Graph[i][j]]++;
         }

     }

     for (int i=; i<rudu.size(); i++)
     {
         if(rudu[i]==)
             Hq.push(i);
     }

     if(Hq.empty())
         return false;

     while(!Hq.empty())
     {
         int tmp = Hq.front();
         Hq.pop();
         for(int i=; i<Graph[tmp].size(); i++)
         {
             rudu[ Graph[tmp][i] ]--;
             if( rudu[ Graph[tmp][i] ]== )
                 Hq.push(Graph[tmp][i]);
         }
     }

     for(int i=; i<rudu.size(); i++)
         if(rudu[i]!=)
             return false;
     return true;
 }

 int main()
 {
     vector<int> edge;
     //vector<vector<int> > Graph(100000, edge);

     vector<bool> res;

     int T, N, M;
     cin>>T;
     while(T--)
     {
         cin>>N>>M;
         vector<vector<int> > Graph(N, edge); //边表

         while(M--)
         {
             int a, b;
             cin>>a>>b;
             a--;   //顶点数从0开始
             b--;
             Graph[a].push_back(b);
         }
         res.push_back(isTuopu(Graph));
     }

     for (int i=; i<res.size(); i++)
     {
         if(res[i])
             cout<<"Correct"<<endl;
         else
             cout<<"Wrong"<<endl;
     }

     return ;

 }