Ex 6_12 凸多边形的最优三角剖分..._第六次作业

假设顶点的总数为n，从0到n-1. 从序号为0的顶点开始以逆时针方向排序，对于

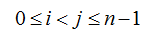
令子问题A[i,j]为包含顶点i,i+1, . . . j的凸多边形的最小三角剖分代价，dist(i,j)为顶点i到顶点j的距离。对于子问题A[i,j],考虑边e(i,j)最终会在某个三角形内，为了找出这个三角形，计算i到j之间的每个顶点k与i和j围成的三角形的对角线的和的最小值即为A[i,j]，找出对角线和的最小值所对应的k,再继续查找A[i,k],A[k,j],直到多边形不能再划分为止，因此的到递推式

 package org.xiu68.ch06.ex6;

 public class Ex6_12 {

     public static Point[] ps1,ps2;
     //凸多边形的最优三角形剖分，求所有对角线之和的最小值
     public static void main(String[] args) {
         // TODO Auto-generated method stub
         /*
          最小三角剖分代价为：8.47213595499958
         三角形划分方式为：
         Point:0,Point:4,Point:1
         Point:1,Point:4,Point:2
         */
         ps1=new Point[]{
                 new Point(2,0),
                 new Point(0,2),
                 new Point(0,4),
                 new Point(4,4),
                 new Point(4,2)
         };
         int[][] arr1=new int[ps1.length][ps1.length];
         minTriangle(ps1,arr1);   //8.47213595499958
         System.out.println("三角形划分方式为：");
         divide(arr1,0,ps1.length-1);

         /*
          最小三角剖分代价为：11.21110255092798
         三角形划分方式为：
         Point:0,Point:5,Point:1
         Point:1,Point:5,Point:3
         */
         System.out.println();
         ps2=new Point[]{
                 new Point(0,2),
                 new Point(10,4),
                 new Point(12,4),
                 new Point(13,2),
                 new Point(12,0),
                 new Point(10,0)
         };
         int[][] arr2=new int[ps2.length][ps2.length];
         minTriangle(ps2,arr2);  //11.21110255092798
         System.out.println("三角形划分方式为：");
         divide(arr2,0,ps2.length-1);
     }

     //B中存放三角形的第三个顶点
     public static void minTriangle(Point[] ps,int[][] B){
         double[][] A=new double[ps.length][ps.length];        //子问题A[i][j]的最优三角剖分代价

         for(int i=0;i<A.length;i++)
             for(int j=0;j<A[i].length;j++){
                 A[i][j]=0;
                 B[i][j]=0;
             }

         for(int s=4;s<=ps.length;s++){                      //包含s个顶点的多边形的最优剖分代价
             for(int i=0;i<ps.length-s+1;i++){                //包含s个顶点的多边形的开始顶点，以逆时针方向前进
                 int j=i+s-1;                                //包含s个顶点的多边形的结束顶点
                 A[i][j]=Double.MAX_VALUE;
                 double temp=A[i][j];

                                                         //t为i和j的相对顶点，从i的后一个顶点开始，结束顶点为j的前一个顶点
                 for(int t=i+1;t<=j-1;t++){
                     if(t==i+1){                         //t为i的后一个顶点
                         temp=dist(ps,t,j)+A[t][j];
                     }
                     else if(t==j-1){                       //t为j的前一个顶点
                         temp=dist(ps,i,t)+A[i][t];
                     }else{                               //t处于i的后一个顶点之后，j的前一个顶点之前
                         temp=dist(ps,i,t)+dist(ps,j,t)+A[i][t]+A[t][j];
                     }
                     if(A[i][j]>temp){
                         A[i][j]=temp;
                         B[i][j]=t;
                     }
                 }//
             }//
         }//
         System.out.println("最小三角剖分代价为："+A[0][ps.length-1]);
     }

     public static void divide(int[][] B,int i,int j){
         if(B[i][j]!=0){
             System.out.println("Point:"+i+",Point:"+j+",Point:"+B[i][j]);
             divide(B,i,B[i][j]);
             divide(B,B[i][j],j);
         }
     }

     //顶点序号i和j之间的距离
     public static double dist(Point[] ps, int i,int j){
         double m1=Math.pow(ps[i].x-ps[j].x, 2);
         double m2=Math.pow(ps[i].y-ps[j].y, 2);
         return Math.sqrt(m1+m2);
     }

 }

 class Point{
     public double x;
     public double y;
     public Point(double x,double y){
         this.x=x;
         this.y=y;
     }
 }