堆模板（pascal）洛谷P3378

题目描述

如题，初始小根堆为空，我们需要支持以下3种操作：

操作1： 1 x 表示将x插入到堆中

操作2： 2 输出该小根堆内的最小数

操作3： 3 删除该小根堆内的最小数

输入输出格式

输入格式：

第一行包含一个整数N，表示操作的个数

接下来N行，每行包含1个或2个正整数，表示三种操作，格式如下：

操作1： 1 x

操作2： 2

操作3： 3

输出格式：

包含若干行正整数，每行依次对应一个操作2的结果。

输入输出样例

输入样例#1：

5
1 2
1 5
2
3
2

输出样例#1：

2
5

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=15

对于70%的数据：N<=10000

对于100%的数据：N<=1000000（注意是6个0。。。不过不要害怕，经过编者实测，堆是可以AC的）

样例说明：

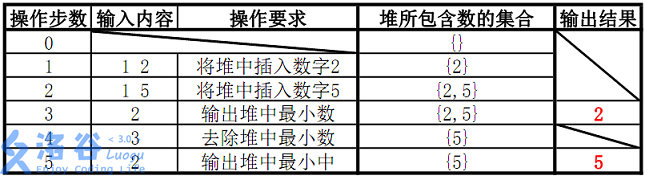
故输出为2、5

明天市赛，继续复习板子。

代码丑勿喷。

 program rrr(input,output);
 var
   a:array[..]of longint;
   n,opt,i,m,t,k,x:longint;
 procedure ins;
 begin
    inc(m);a[m]:=x;k:=m;
    while (k>) and (a[k>>]>a[k]) do begin t:=a[k>>];a[k>>]:=a[k];a[k]:=t;k:=k>>; end;
 end;
 procedure del;
 begin
    a[]:=a[m];dec(m);k:=;
    while true do
       begin
          if k+k>m then exit;
          if k+k=m then
             begin
                if a[k+k]<a[k] then begin t:=a[k+k];a[k+k]:=a[k];a[k]:=t; end;
                break;
             end;
          if (a[k+k]>=a[k]) and (a[k+k+]>=a[k]) then break;
          if a[k+k]<a[k+k+] then
             begin t:=a[k+k];a[k+k]:=a[k];a[k]:=t;k:=k+k; end
         else begin t:=a[k+k+];a[k+k+]:=a[k];a[k]:=t;k:=k+k+; end;
       end;
 end;
 begin
    assign(input,'r.in');assign(output,'r.out');reset(input);rewrite(output);
    readln(n);
    m:=;
    for i:= to n do
       begin
          read(opt);
          if opt= then begin read(x);ins; end
          else if opt= then writeln(a[])
          else del;
       end;
    close(input);close(output);
 end.