用Python实现求Fibonacci数列的第n项

1. 背景——Fabonacci数列的介绍（摘自百度百科）：

　　斐波那契数列（Fibonacci sequence），又称黄金分割数列。因数学家列昂纳多·斐波那契（Leonardoda Fibonacci ）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……用公式定义如下：

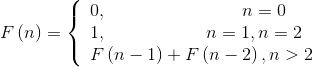
计算通式为：

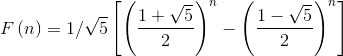
当n趋向于无穷大时，前一项与后一项的比值越来越逼近黄金分割0.618

2. 用Python迭代实现求解Fibonacci数列的第n项

def fib_iter(n):
    n1 = 1
    n2 = 1
    n3 = 1

    if (n < 1):
        print("Wrong input! ")
        return -1
    else:
        while (n-2) > 0:
            n3 = n2 + n1
            n1 = n2
            n2 = n3
            n -= 1

    return n3

result = fib_iter(35)
if result != -1:
    print(result)

优点：当n数值较大时，求解速度较递归法快

缺点：代码不简洁易懂

3. 用Python递归实现求解Fibonacci数列的第n项

def fib_re(n):
    result = 0
    if(n < 1):
        print("Wrong input! ")
        return -1
    else:
        if(n == 1 or n == 2):
            return 1
        else:
            return fib_re(n-1) + fib_re(n-2)

result = fib_re(35)
if result != -1:
    print(result)

#分治思想

优点：代码简洁易懂

缺点：当n数值较大时，反复的出栈和压栈操作使得运行时间很长