L1、L2损失函数、Huber损失函数

L1范数损失函数，也被称为最小绝对值偏差（LAD），最小绝对值误差（LAE）

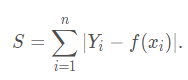
L2范数损失函数，也被称为最小平方误差（LSE）

L2损失函数	L1损失函数
不是非常的鲁棒（robust）	鲁棒
稳定解	不稳定解
总是一个解	可能多个解

鲁棒性

最小绝对值偏差之所以是鲁棒的，是因为它能处理数据中的异常值。如果需要考虑任一或全部的异常值，那么最小绝对值偏差是更好的选择。

L2范数将误差平方化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数来得大，因此模型会对这个样本更加敏感，这就需要调整模型来最小化误差。如果这个样本是一个异常值，模型就需要调整以适应单个的异常值，这会牺牲许多其它正常的样本，因为这些正常样本的误差比这单个的异常值的误差小。

稳定性

最小绝对值偏差方法的不稳定性意味着，对于数据集的一个小的水平方向的波动，回归线也许会跳跃很大。

相反地，最小平方法的解是稳定的，因为对于一个数据点的任何微小波动，回归线总是只会发生轻微移动

总结

MSE对误差取了平方，如果存在异常值，那么这个MSE就很大。

MAE更新的梯度始终相同，即使对于很小的值，梯度也很大，可以使用变化的学习率。MSE就好很多，使用固定的学习率也能有效收敛。

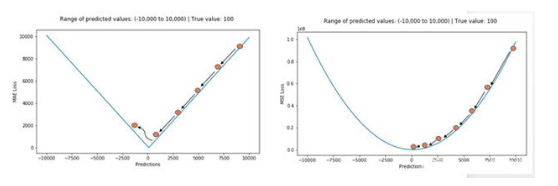
总而言之，处理异常点时，L1损失函数更稳定，但它的导数不连续，因此求解效率较低。L2损失函数对异常点更敏感，但通过令其导数为0，可以得到更稳定的封闭解。

Huber

l1和l2都存在的问题：

若数据中90%的样本对应的目标值为150，剩下10%在0到30之间。

那么使用MAE作为损失函数的模型可能会忽视10%的异常点，而对所有样本的预测值都为150，因为模型会按中位数来预测；

MSE的模型则会给出很多介于0到30的预测值，因为模型会向异常点偏移。

这些情况下最简单的办法是对目标变量进行变换。而另一种办法则是换一个损失函数，这就引出了下面要讲的第三种损失函数，即Huber损失函数。

Huber损失，平滑的平均绝对误差

Huber损失对数据中的异常点没有平方误差损失那么敏感。

本质上，Huber损失是绝对误差，只是在误差很小时，就变为平方误差。误差降到多小时变为二次误差由超参数δ（delta）来控制。当Huber损失在[0-δ,0+δ]之间时，等价为MSE，而在[-∞,δ]和[δ,+∞]时为MAE。

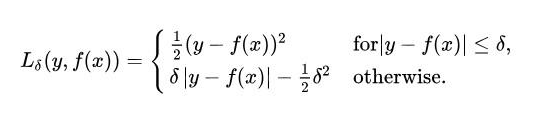
Huber损失结合了MSE和MAE的优点，对异常点更加鲁棒。