PAT甲级——A1123 Is It a Complete AVL Tree【30】

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

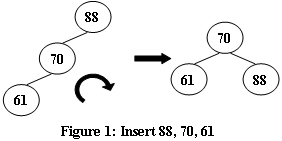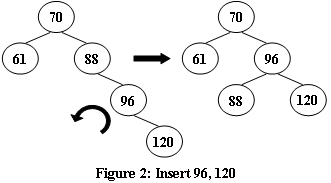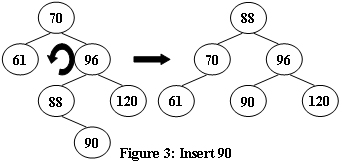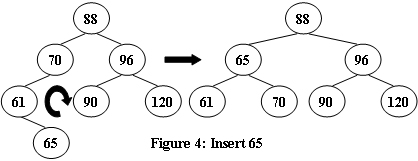Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YESif the tree is complete, or NO if not.

Sample Input 1:

5
88 70 61 63 65

Sample Output 1:

70 63 88 61 65
YES

Sample Input 2:

8
88 70 61 96 120 90 65 68

Sample Output 2:

88 65 96 61 70 90 120 68
NO

分析：这道题考察AVL树和层序遍历以及完全二叉树
判断是不是完全⼆叉树，就看在出现了⼀个孩⼦为空的结点之后是否还会出现孩⼦结点不为空的结
点，如果出现了就不是完全⼆叉树。
AVL树⼀共有四种情况，这⾥我把发现树不平衡的那个结点叫做A结点，A发现树不平衡的情况有四
种：
新来的结点插⼊到A的左⼦树的左⼦树
新来的结点插⼊到A的左⼦树的右⼦树
新来的结点插⼊到A的右⼦树的左⼦树
新来的结点插⼊到A的右⼦树的右⼦树
发现不平衡时就需要处理，第1种情况只要简单的右旋，第4种情况只需左旋⼀下，
第2种情况需要先对A的左⼦树左旋⼀下，然后对A右旋，同理第3种情况需要对A的右⼦树右旋⼀下，然后对A左旋

 #include <iostream>
 #include <vector>
 #include <queue>
 #include <algorithm>
 using namespace std;
 struct Node
 {
     int v;
     Node *l, *r;
     Node(int a = -) :v(a), l(nullptr), r(nullptr) {}
 };
 int n, a;
 vector<int>res;
 int getHeight(Node* root)
 {
     if (root == nullptr)
         return ;
     return max(getHeight(root->l), getHeight(root->r))+;
 }
 Node* rotateRight(Node* root)//右旋
 {
     Node*p = root->l;
     root->l = p->r;
     p->r = root;
     return p;//新的根节点
 }
 Node* rotateLeft(Node* root)//左旋
 {
     Node*p = root->r;
     root->r = p->l;
     p->l = root;
     return p;//新的根节点
 }
 Node* rotateLeftRight(Node* root)//左右旋
 {
     root->l = rotateLeft(root->l);//先左旋
     return rotateRight(root);//再右旋
 }
 Node* rotateRightLeft(Node* root)//右左旋
 {
     root->r = rotateRight(root->r);//先右旋
     return rotateLeft(root);//再左旋
 }
 Node* Insert(Node* root, int x)
 {
     if (root == nullptr)
     {
         root = new Node(x);
         return root;
     }
     if (x < root->v)
     {
         root->l = Insert(root->l, x);
         if (getHeight(root->l) - getHeight(root->r) >= )
             root = x < root->l->v ? rotateRight(root) : rotateLeftRight(root);
     }
     else
     {
         root->r = Insert(root->r, x);
         if (getHeight(root->r) - getHeight(root->l) >= )
             root = x > root->r->v ? rotateLeft(root) : rotateRightLeft(root);
     }
     return root;
 }
 bool LevelOrder(Node* root)
 {
     bool flag = true;//是不是完全二叉树
     if (root == nullptr)
         return flag;
     queue<Node*>q, temp;
     q.push(root);
     while (!q.empty())
     {
         Node*p = q.front();
         q.pop();
         temp.push(p);
         res.push_back(p->v);
         if (p->l != nullptr)
             q.push(p->l);
         else if (temp.size() + q.size() != n)//中间出现空节点，不是完全二叉树
             flag = false;
         if (p->r != nullptr)
             q.push(p->r);
         else if (temp.size() + q.size() != n)//中间出现空节点，不是完全二叉树
             flag = false;
     }
     return flag;
 }
 int main()
 {
     cin >> n;
     Node* root = nullptr;
     for (int i = ; i < n; ++i)
     {
         cin >> a;
         root = Insert(root, a);
     }
     bool flag = LevelOrder(root);
     for (int i = ; i < res.size(); ++i)
         cout << (i >  ? " " : "") << res[i];
     if (flag)
         cout << endl << "YES" << endl;
     else
         cout << endl << "NO" << endl;
     return ;
 }