NOIP做题练习（day3）

A - 军队

问题描述

给定一个有 $n$ 个队伍的人组成的序列，第 $i$ 个队伍 $i$ 有 $s[i]$个人组成，一个 $l$ 到 $r$的子序列是合法的，当且仅当$((∀i)(∀j)∧(i≠j)∧(l≤i,j≤r))→(gcd(s[i],s[j])=1)$，即对于该序列中任两个不相同的队伍，他们人数的最大公约数为 $1$，并且要求该子序列的总人数大于等于 $k$。

且由于每个队伍能够审批携带的仪器是有限的，所以需要这个队伍$(r - l + 1)$尽可能长，请求出这个队伍的最长长度，若不存在，请输出 $0$。

输入

第一行两个整数 $n,k$ 分别表示队伍数量和人数下限

接下来一行 $n$ 个整数，表示每个队伍的人数

输出

一行一个整数，表示队伍的最长长度，如果不存在一个这样的队伍，则输出 $0$

输入输出样例

样例输入

5 14

4 5 12 3 2

样例输出

数据范围

对于 $10\%$的数据 $n≤10$

对于另外 $20\%$的数据 $n≤100$

对于另外 $20\%$的数据 $n≤2\times 1000$

对于全部的数据 $1≤n≤10^5, 1≤s[i]≤10^6, k≤ int$。

题解

枚举左端点及右端点即可，还要加一些玄学优化。

$n$方过十万！

代码

#include <iostream>

#include <cstdio>

#include <cstdlib>

#include <cstring>

#include <algorithm>

#include <cmath>

#include <cctype>

#define int long long

#define gI gi

#define itn int

#define File(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)

using namespace std;

inline int gi()

{

    int f = 1, x = 0; char c = getchar();

    while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}

    while (c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();}

    return f * x;

}

int n, k, a[100003], dp[100003], sum[100003];

namespace sub1

{

	int gcd(int a, int b)

	{

		if (b == 0) return a;

		return gcd(b, a % b);

	}

	bool pd(int l, int r)

	{

		for (int i = l; i <= r; i+=1)

		{

			for (int j = i + 1; j <= r; j+=1)

			{

				if (a[i] % 2 == 0 && a[j] % 2 == 0) return false;

				if (gcd(a[i], a[j]) != 1) return false;

			}

		}

		return true;

	}

	void getans()

	{

		itn ans = 0;

		for (int i = 1; i <= n; i+=1)

		{

			for (int j = i + 1; j <= n; j+=1)

			{

				if (sum[j] - sum[i - 1] < k) continue;

				if (pd(i, j)) ans = max(ans, j - i + 1);

			}

		}

		printf("%lld\n", ans);

		return;

	}

}

namespace sub2

{

	int gcd(int a, int b)

	{

		if (b == 0) return a;

		return gcd(b, a % b);

	}

	void getans()

	{

		int ans = 0;

		for (int i = 1; i <= n; i+=1)

		{

			int Right;

			for (Right = i; Right <= n; Right+=1) if (sum[Right] - sum[i] >= k) break;

			bool fl = false;

			for (int j = i; j <= Right && !fl; j+=1)

			{

				for (int k = j + 1; k <= Right && !fl; k+=1)

				{

					if (gcd(a[j], a[k]) != 1) fl = true;

				}

			}

			if (fl) continue;

			ans = max(ans, Right - i + 1);

			for (++Right; Right <= n; Right+=1)

			{

				bool fl = false;

				for (int j = i; j < Right && !fl; j+=1) if (gcd(a[j], a[Right]) != 1) fl = true;

				if (fl) break;

				ans = max(ans, Right - i + 1);

			}

		}

		printf("%lld\n", ans);

	}

}

signed main()

{

	File("tarmy");

	n = gi(), k = gi();

	for (int i = 1; i <= n; i+=1) a[i] = gi(), sum[i] = sum[i - 1] + a[i];

	if (sum[n] < k) {puts("0"); return 0;}

	if (n <= 100) {sub1::getans(); return 0;}

	else {sub2::getans(); return 0;}

	return 0;

}

B - 取石块儿

问题描述

小 $L$ 和小 $T $进行取石块儿游戏，给定一个整数 $n$ 表示石块儿总数，给定一个整数 $k$ 表

示每次最多能拿走的石块儿数量，小 $L$ 先手，每次能拿走 $1$~$k$ 个石块儿，他们中总会有一

个人最后拿走 $s$ 块儿石块儿，使得剩余石块儿数量为 $0$，则最后一个拿走剩下石块儿的人获

胜，另外一个人失败。

小 $T$ 非常聪明，小 $L$ 绝顶(秃子(逃))聪明，请判断小 $T$ 是否能取胜。

输入

第一行一个整数 $T$ 表示数据组数，接下来 $T$ 行每行两个整数 $n$,$k$ 意义为描述所给。

输出

对于每组数据，输出"$YES$"或者"$NO$"(不带引号)，代表小 $T$ 是否能够获胜。

输入输出样例

样例输入

样例输出

YES

YES

数据范围

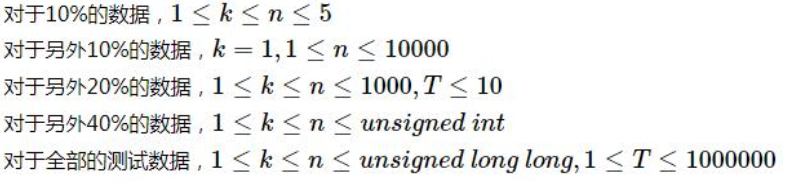
题解

首先对于只有$k$个石块儿的情况，很明显直接一次拿走就能获胜，对于有$k + 1$块石块儿情况，不论怎么拿，总会产生少于$k$块石块儿的情况，于是是必败的。

同样，对于$(k + 1, k + k + 1]$个石块儿的情况，总能拿走一部分石块儿是的对手处于$k + 1$的必败情况，归纳证明当$n \% (k + 1) == 0$的时候，先手必胜，反之后手必胜。

代码超短的……

代码

#include <iostream>

#include <cstdio>

#include <cstdlib>

#include <cstring>

#include <algorithm>

#include <cmath>

#include <cctype>

#define int unsigned long long

#define gI gi

#define itn int

#define File(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)

using namespace std;

inline int gi()

{

    int f = 1, x = 0; char c = getchar();

    while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}

    while (c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();}

    return f * x;

}

int t, n, k, a, b;

signed main()

{

	File("tstones");

	t = gi();

	while (t--)

	{

		n = gi(), k = gi();

		if (k == 1)

		{

			if (n & 1) puts("NO");

			else puts("YES");

		}

		else

		{

			if (n % (k + 1)) puts("NO");

			else puts("YES");

		}

	}

	return 0;

}

总结

这次练习做得不是很好。

要拿的很多部分分都没有拿到。

还要继续努力啊$QwQ$。