不一样的LCA——luoguP1852跳跳棋

Problem：

洛谷端题目链接

loj端题目链接

题目大意：

在一条数轴上进行跳跳棋游戏。棋子只能摆在整点上。每个点不能摆超过一个棋子。用跳跳棋完成：棋盘上有3颗棋子，分别在a，b，c这三个位置。我们要通过最少的跳动把他们的位置移动成x，y，z。

跳动的规则：任意选一颗棋子，对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。如果可以完成输出YES以及所需步数，如果不行输出NO即可。

对，只允许跳过一颗棋子（因为这个想了好久自闭了）

---

Solution：

看完题目之后第一反应是不是：woc这什么，跟LCA有什么关系？？这哪来的树？？

那就对了（%dalao）

分类讨论，发现对于每一种合法的状态（也就是没有棋子重合）只有三种情况能走

1.中点（y）向左边跳

2.中点（y）向右边跳

3.左边（或者右边）往中间跳 =>可以证明由于只能跳过一颗棋子，在d1!=d2时只能走一个

这好像有点像二叉树？（将1.2看做子节点，3看做父亲节点）

对于1.2情况，我们可以发现（以下以1为例）：

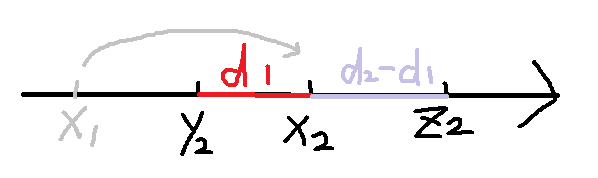
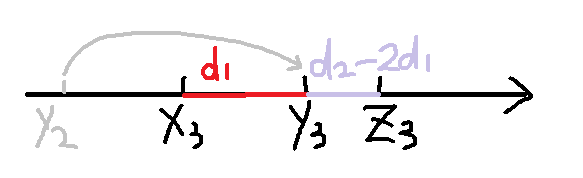
可以知道，d1>d2时左边的棋子不能跳了，我们最多走d2/d1步，此时d2小于d1了换个方向走，当d2%d1等于0时走d2/d1-1步就到根了。

所以根据这个，我们可以求出开始状态与结束状态的祖先，判断他们的祖先是否相等 =>因为祖先相同就可以通过相反操作得到

这个操作模拟一下就好了，我们可以用除来加快跳(（一个个跳会超时的）

模拟部分：

                 int d1=y-x;
         int d2=z-y;
         if(d1<d2)
         {
             int step=d2/d1;
             if(d2%d1==)    step--;
             if(step>dis)    step=dis;
             x+=step*d1;
             y+=step*d1;
             if(x>y)    swap(x,y);
             dis-=step;
         }
         else
         {
             int step=d1/d2;
             if(d1%d2==)    step--;
             if(step>dis)    step=dis;
             z-=d2*step;
             y-=d2*step;
             if(z<y)    swap(z,y);
             dis-=step;
         }        

找到了公共祖先之后就可以二分查找（查找往上跳的步数）　

l是0，r是min(结果与公共祖先的距离，起点与公共祖先的距离)

                 int l=,r=min(dep1,dep2),step=;
             while(l<=r)
         {
             int mid=l+r>>;
             b1=go(st,mid);
             b2=go(ed,mid);
             if(pd(b1,b2))    step=mid,r=mid-;
             else    l=mid+;
         }      

以上是我认为的核心内容（看不懂就感性理解一下）

---

#include<iostream>
#include<cstdio>
using namespace std;
struct node{
    int x,y,z;
}st,ed,b1,b2;
int dep1,dep2;
inline int read(){
    char ch;
    int sign=;
    while((ch=getchar())<''||ch>'')
        if(ch=='-')    sign=-;
    int res=ch-'';
    while((ch=getchar())>=''&&ch<='')
        res=res*+ch-'';
    return res*sign;
}
inline void sort(node &x){
    if(x.x>x.y)    swap(x.x,x.y);
    if(x.x>x.z)    swap(x.x,x.z);
    if(x.y>x.z)    swap(x.y,x.z);
}
inline int findfather(node &b){
    int res=;
    sort(b);
    while(b.x+b.z!=b.y*){
        int d1=b.y-b.x;
        int d2=b.z-b.y;
        if(d1<d2){
            int step=d2/d1;
            if(d2%d1==)    step--;
            b.x+=step*d1;
            b.y+=step*d1;
            if(b.x>b.y)    swap(b.x,b.y);
            res+=step;
            }else{
            int step=d1/d2;
            if(d1%d2==)    step--;
            b.z-=step*d2;
            b.y-=step*d2;
            if(b.y>b.z)    swap(b.y,b.z);
            res+=step;
        }
    }
    return res;
}
inline bool pd(node x,node y){
    if(x.x==y.x&&x.y==y.y&&x.z==y.z)    return true;
    return false;
}
inline int abs(int x){
    return x>=?x:-x;
}
inline node go(node b,int dis){
    sort(b);
    while(dis){
        int d1=b.y-b.x;
        int d2=b.z-b.y;
        if(d1<d2){
            int step=d2/d1;
              if(d2%d1==)    step--;
            if(step>dis)    step=dis;
            b.x+=step*d1;
            b.y+=step*d1;
            if(b.x>b.y)    swap(b.x,b.y);
            dis-=step;
        }else{
            int step=d1/d2;
            if(d1%d2==)    step--;
            if(step>dis)    step=dis;
            b.z-=d2*step;
            b.y-=d2*step;
            if(b.z<b.y)    swap(b.z,b.y);
            dis-=step;
        }
    }
    return b;
}
int main(){
    st.x=read();st.y=read();st.z=read();
    ed.x=read();ed.y=read();ed.z=read();
    sort(st);sort(ed);
    b1=st;b2=ed;
    dep1=findfather(b1);
    dep2=findfather(b2);
    if(!pd(b1,b2)){
        printf("NO\n");
        return ;
    }else{
        int c=abs(dep1-dep2);
        if(dep1<dep2)
            ed=go(ed,c);
        else if(dep1>dep2)
            st=go(st,c);
        int l=,r=min(dep1,dep2),step=;
        while(l<=r){
            int mid=l+r>>;
            b1=go(st,mid);
            b2=go(ed,mid);
            if(pd(b1,b2))    step=mid,r=mid-;
            else    l=mid+;
        }
        printf("YES\n");
        printf("%d",step*+c);
    }
    return ;
}

complete code