Morley's Theorem （计算几何基础+向量点积、叉积、旋转、夹角等+两直线的交点）

题目链接：https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2119

题面：Morleys theorem states that that the lines trisecting the angles of an arbitrary plane triangle meet at the vertices of an equilateral triangle. For example in the figure below the tri-sectors of angles A, B and C has intersected and created an equilateral triangle DEF. Of course the theorem has various generalizations, in particular if all of the trisectors are intersected one obtains four other equilateral triangles. But in the original theorem only tri-sectors nearest to BC are allowed to intersect to get point D, tri-sectors nearest to CA are allowed to intersect point E and tri-sectors nearest to AB are intersected to get point F. Trisector like BD and CE are not allowed to intersect. So ultimately we get only one equilateral triangle DEF. Now your task is to find the Cartesian coordinates of D, E and F given the coordinates of A, B, and C.
Input
First line of the input file contains an integer N (0 < N < 5001) which denotes the number of test cases to follow. Each of the next lines contain six integers XA,YA,XB,YB,XC,YC. This six integers actually indicates that the Cartesian coordinates of point A, B and C are (XA,YA),(XB,YB) and (XC,YC) respectively. You can assume that the area of triangle ABC is not equal to zero, 0 ≤ XA,YA,XB,YB,XC,YC ≤ 1000 and the points A, B and C are in counter clockwise order.
Output
For each line of input you should produce one line of output. This line contains six floating point numbers XD,YD,XE,YE,XF,YF separated by a single space. These six floating-point actually means that the Cartesian coordinates of D, E and F are (XD,YD),(XE,YE) ,(XF,YF) respectively. Errors less than 10−5 will be accepted.
Sample Input
2

1 1 2 2 1 2

0 0 100 0 50 50
Sample Output
1.316987 1.816987 1.183013 1.683013 1.366025 1.633975

56.698730 25.000000 43.301270 25.000000 50.000000 13.397460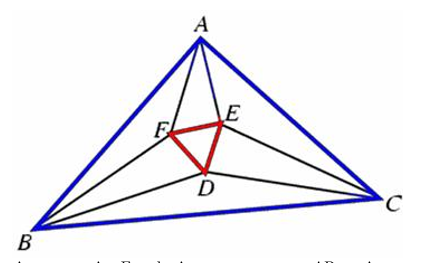

思路：本题为一道比较简单的计算几何入门题，运用了很多的计算几何知识，不过只要想通如何求DEF的话，就只需通过套用模板即可解决

代码实现如下：

 #include <cstdio>
 #include <cmath>
 using namespace std;

 struct Point{
     double x,y;
     Point(double x = , double y = ) : x(x), y(y) {}
 };

 typedef Point Vector;

 int t;
 Point A, B, C, D, E, F;

 Vector operator + (Vector A, Vector B){
     return Vector(A.x + B.x, A.y + B.y);
 }

 Vector operator - (Vector A, Vector B){
     return Vector(A.x - B.x, A.y - B.y);
 }

 Vector operator * (Vector A, double p){
     return Vector(A.x * p, A.y * p);
 }

 Vector operator / (Vector A, double p){
     return Vector(A.x / p, A.y / p);
 }

 double Dot(Vector A, Vector B){
     return A.x * B.x + A.y * B.y;
 }

 double Length(Vector A){
     return sqrt(Dot(A, A));
 }

 double Angle(Vector A, Vector B){
     return acos(Dot(A, B) / Length(A) / Length(B));
 }

 Vector Rotate(Vector A, double rad){
     return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
 }

 double Cross(Vector A, Vector B){
     return A.x * B.y - A.y * B.x;
 }

 Point GetLineIntersection(Point P, Vector v, Point Q, Vector w){
     Vector u = P - Q;
     double t = Cross(w, u) / Cross(v, w);
     return P + v * t;
 }

 Point GetD(Point A, Point B, Point C){
     Vector v1 = C - B;
     double a1 = Angle((A - B), v1);
     v1 = Rotate(v1, a1 / );

     Vector v2 = B - C;
     double a2 = Angle((A - C), v2);
     v2 = Rotate(v2, -a2 / );

     return GetLineIntersection(B, v1, C, v2);
 }

 int main(){
     scanf("%d", &t);
     while(t--){
         scanf("%lf%lf%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y, &C.x, &C.y);
         D = GetD(A, B, C);
         E = GetD(B, C, A);
         F = GetD(C, A, B);
         printf("%.6f %.6f %.6f %.6f %.6f %.6f\n", D.x, D.y, E.x, E.y, F.x, F.y);
     }
 }