hdu-5714 拍照(二分)

题目链接：

拍照

Time Limit: 6000/3000 MS (Java/Others)   

 Memory Limit: 65536/65536 K (Java/Others)

Problem Description

 

小明在旅游的路上看到了一条美丽的河，河上有许多船只，有的船只向左航行，有的船只向右航行。小明希望拍下这一美丽的风景，并且把尽可能多的船只都完整地拍到一张照片中。

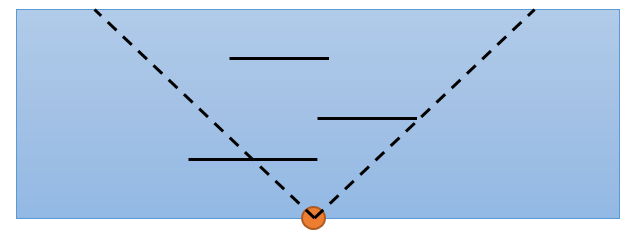
小明位于河的边上，并且可以在河边的任意位置进行拍照，照相机的视野恰好为90度角，只能以垂直于河边的方向进行拍照。河上的船只全都可看作是平行于河边的一条线段，跟河边的距离各不相同，有的正在向左移动，有的正在向右移动，但移动速度恰好都是一样的。小明可以等待恰当的时间让尽量多的船只都走进照相机的视野里，你不需要考虑船只之间会互相遮挡视野的情况。


 

Input

 

第一行为T，表示输入数据组数。

下面T组数据，对于每组数据：

第一行是一个数n(1≤n≤10^4)，表示船只的数量。

接下来n行，每行四个整数
x,y,z,d(−10^6≤x<y≤10^6,1≤z≤10^4)，表示船只的左端点位置、右端点位置、距离河边的距离，以及航行的方向。d为−1表示向左航行，1表示向右航行。

 

Output

 

对第i组数据，输出

Case #i:

然后输出一行，仅包含一个整数，表示最多可以拍到多少完整的船只。

 

Sample Input

 

3

2

1 3 1 1

2 4 1 -1

2

1 3 1 -1

2 4 1 1

1

1 4 1 1

 

Sample Output

 

Case #1:

2

Case #2:

1

Case #3:

0

 

题意：

 

 

思路：

 

[y-z,x+z]为岸上能看到这艘船的位置,这是一条线段,update(l,1)update(r+1,-1),然后就可以对于每一点可以query这点能看到的船的数量了;

范围太大,就可以把 这些线段离散化,只保留他们的端点,然后把这些端点的范围离散到[1,2*N]的范围内,大小的关系不变;

当然向左走和向右走的船要分开update,query;

最后得到答案后就要找最大值了,对于任意的一点,它能看到的最大的船的数目是这点后面所有点能看到的向左走的船的最大数目+这点之前所有点能看到的向右走的船的最大数目;

 

还有就是这个没必要用树状数组,可以直接最后扫一遍就可以得到每个点的能看到的船的数目了;

 

 

 

AC代码：

 

 

//#include <bits/stdc++.h>
//有树状数组的
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<''||CH>'';F= CH=='-',CH=getchar());
    for(num=;CH>=''&&CH<='';num=num*+CH-'',CH=getchar());
    F && (num=-num);
}
int stk[], tp;
template<class T> inline void print(T p) {
    if(!p) { puts(""); return; }
    while(p) stk[++ tp] = p%, p/=;
    while(tp) putchar(stk[tp--] + '');
    putchar('\n');
}

const LL mod=1e9+;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=1e4+;

int n,sum[][*N],a[*N],b[*N],pre[*N],nex[*N];
int num,mmax;

struct node
{
    int l,r,d;
}po[*N];

int findpos(int x)
{
    int l=,r=mmax;
    while(l<=r)
    {
        int mid=(l+r)>>;
        if(b[mid]<x)l=mid+;
        else r=mid-;
    }
    return l;
}

int lowbit(int x)
{
    return x&(-x);
}
void update(int x,int y,int flag)
{
    while(x<=mmax)
    {
        sum[flag][x]+=y;
        x+=lowbit(x);
    }
}
int query(int x,int flag)
{
    int s=;
    while(x>)
    {
        s+=sum[flag][x];
        x-=lowbit(x);
    }
    return s;
}

int main()
{
      int t;
      read(t);
      int Case=;
      while(t--)
      {
          mst(sum,);
          int x,y,z,d,cnt=;
          num=;
          mmax=;

          read(n);
          Riep(n)
          {
              read(x),read(y),read(z),read(d);
              if(x+z<y-z)continue;
              po[cnt].l=y-z;
              po[cnt].r=x+z;
              if(d==-)po[cnt++].d=;
              else po[cnt++].d=d;
              a[++num]=y-z;
              a[++num]=x+z;
          }
          sort(a+,a+num+);
          b[++mmax]=a[];
          for(int i=;i<=num;i++)
          {
              if(a[i]!=a[i-])b[++mmax]=a[i];
          }

          for(int i=;i<cnt;i++)
          {
              po[i].l=findpos(po[i].l);
              po[i].r=findpos(po[i].r);
              update(po[i].l,,po[i].d);
              update(po[i].r+,-,po[i].d);
          }
          for(int i=;i<=mmax;i++)
          {
              pre[i]=max(query(i,),pre[i-]);
              nex[i]=query(i,);
          }
          int ans=;
          nex[mmax+]=;
          for(int i=mmax;i>;i--)
          {
              nex[i]=max(nex[i+],nex[i]);
              ans=max(ans,pre[i]+nex[i]);
          }
          printf("Case #%d:\n",Case++);
          print(ans);
      }
    return ;
}

//#include <bits/stdc++.h>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<''||CH>'';F= CH=='-',CH=getchar());
    for(num=;CH>=''&&CH<='';num=num*+CH-'',CH=getchar());
    F && (num=-num);
}
int stk[], tp;
template<class T> inline void print(T p) {
    if(!p) { puts(""); return; }
    while(p) stk[++ tp] = p%, p/=;
    while(tp) putchar(stk[tp--] + '');
    putchar('\n');
}

const LL mod=1e9+;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=1e4+;

int n,sum[][*N],a[*N],b[*N],pre[*N],nex[*N],sum1[*N],sum2[*N];
int num,mmax;

struct node
{
    int l,r,d;
}po[*N];

int findpos(int x)
{
    int l=,r=mmax;
    while(l<=r)
    {
        int mid=(l+r)>>;
        if(b[mid]<x)l=mid+;
        else r=mid-;
    }
    return l;
}

int main()
{
      int t;
      read(t);
      int Case=;
      while(t--)
      {
          mst(sum,);
          int x,y,z,d,cnt=;
          num=;
          mmax=;

          read(n);
          Riep(n)
          {
              read(x),read(y),read(z),read(d);
              if(x+z<y-z)continue;
              po[cnt].l=y-z;
              po[cnt].r=x+z;
              if(d==-)po[cnt++].d=;
              else po[cnt++].d=d;
              a[++num]=y-z;
              a[++num]=x+z;
          }
          sort(a+,a+num+);
          b[++mmax]=a[];
          for(int i=;i<=num;i++)
          {
              if(a[i]!=a[i-])b[++mmax]=a[i];
          }

          for(int i=;i<cnt;i++)
          {
              po[i].l=findpos(po[i].l);
              po[i].r=findpos(po[i].r);
              sum[po[i].d][po[i].l]++;
              sum[po[i].d][po[i].r+]--;
          }
          for(int i=;i<=mmax;i++)
          {
              sum1[i]=sum1[i-]+sum[][i];
              sum2[i]=sum2[i-]+sum[][i];
              nex[i]=sum1[i];
              pre[i]=max(pre[i-],sum2[i]);
          }
          int ans=;
          nex[mmax+]=;
          for(int i=mmax;i>;i--)
          {
              nex[i]=max(nex[i+],nex[i]);
              ans=max(ans,pre[i]+nex[i]);
          }
          printf("Case #%d:\n",Case++);
          print(ans);
      }
    return ;
}