论文解读（NGCF）《LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation》

论文信息

论文标题：LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
论文作者：Xiangnan He, Kuan Deng, Xiang Wang, Yan Li, Yongdong Zhang, Meng Wang
论文来源：2020, SIGIR
论文地址：download 
论文代码：download

1 Introduction

　　舍弃了GCN的特征变换（feature transformation）和非线性激活（nonlinear activation），只保留了领域聚合（neighborhood aggregation ）。

2 Prelimiaries

　　NGCF 利用用户项交互图来传播嵌入如下：

　　　　$\begin{array}{l}\mathbf{e}_{u}^{(k+1)}=\sigma\left(\mathbf{W}_{1} \mathbf{e}_{u}^{(k)}+\sum\limits _{i \in \mathcal{N}_{u}} \frac{1}{\sqrt{\left|\mathcal{N}_{u} \| \mathcal{N}_{i}\right|}}\left(\mathbf{W}_{1} \mathbf{e}_{i}^{(k)}+\mathbf{W}_{2}\left(\mathbf{e}_{i}^{(k)} \odot \mathbf{e}_{u}^{(k)}\right)\right)\right) \\\mathbf{e}_{i}^{(k+1)}=\sigma\left(\mathbf{W}_{1} \mathbf{e}_{i}^{(k)}+\sum\limits _{u \in \mathcal{N}_{i}} \frac{1}{\sqrt{\left|\mathcal{N}_{u} \| \mathcal{N}_{i}\right|}}\left(\mathbf{W}_{1} \mathbf{e}_{u}^{(k)}+\mathbf{W}_{2}\left(\mathbf{e}_{u}^{(k)} \odot \mathbf{e}_{i}^{(k)}\right)\right)\right)\end{array}$

　　其中

• • $\mathbf{e}_{u}^{(k)}$ 和 $\mathbf{e}_{i}^{(k)}$ 分别用户 $u$ 和物品 $i$ 在第 $k$ 层的嵌入；
  • $\sigma$ 代表着非线性激活函数；
  • $\mathcal{N}_{u}$ 代表着和用户 $u$ 相关联的物品；
  • $\mathcal{N}_{i} $ 代表着和物品 $i$ 相关联的用户；
  • $\mathbf{W}_{1}$ 和 $\mathbf{W}_{2}$ 代表着各层的权重矩阵；
  • $\left(\mathbf{e}_{u}^{(0)}, \mathbf{e}_{u}^{(1)}, \ldots, \mathbf{e}_{u}^{(L)}\right)$ 代表着各层的用户嵌入；
  • $\left(\mathbf{e}_{i}^{(0)}, \mathbf{e}_{i}^{(1)}, \ldots, \mathbf{e}_{i}^{(L)}\right) $ 代表着各层的物品嵌入；

　　接下来，对比不使用特征转换（feature transformation）和非线性激活函数（non-linear activation function）：

• • $NGCF-f$, which removes the feature transformation matrices $\mathbf{W}_{1}$ and $\mathbf{W}_{2}$ .
  • $NGCF-n$, which removes the non-linear activation function $\sigma $.
  • $NGCF-fn$, which removes both the feature transformation matrices and non-linear activation function.

　　实验：

　　

　　

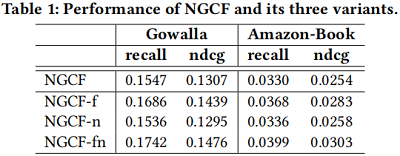
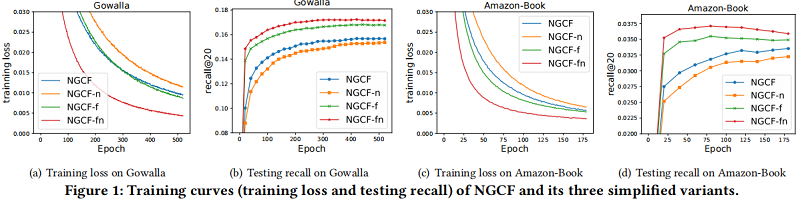
3 Method

3.1 LightGCN

　　它迭代地进行图卷积，即将邻居的特征聚合为目标节点的新表示。这种邻域聚合可以抽象为：

　　　　$\mathbf{e}_{u}^{(k+1)}=\mathrm{AGG}\left(\mathbf{e}_{u}^{(k)},\left\{\mathbf{e}_{i}^{(k)}: i \in \mathcal{N}_{u}\right\}\right) \quad\quad\quad(2)$

3.1.1 Light Graph Convolution (LGC)

　　在 LightGCN中，我们采用简单加权和聚合器，不再使用特征变换和非线性激活。LightGCN 中的图卷积运算定义为：

　　　　${\large \begin{array}{l}\mathbf{e}_{u}^{(k+1)}=\sum\limits _{i \in \mathcal{N}_{u}} \frac{1}{\sqrt{\left|\mathcal{N}_{u}\right|} \sqrt{\left|\mathcal{N}_{i}\right|}} \mathbf{e}_{i}^{(k)} \\\mathbf{e}_{i}^{(k+1)}=\sum\limits _{u \in \mathcal{N}_{i}} \frac{1}{\sqrt{\left|\mathcal{N}_{i}\right|} \sqrt{\left|\mathcal{N}_{u}\right|}} \mathbf{e}_{u}^{(k)}\end{array}} \quad\quad\quad(3)$

　　其中，$\frac{1}{\sqrt{\left|\mathcal{N}_{u}\right|} \sqrt{\left|\mathcal{N}_{i}\right|}}$  是对称标准化项。

　　LGC 只聚合已连接的邻居，而不集成目标节点本身（即自连接）。与 GCN 不同，后者通常聚合扩展的邻居，需要特别处理自连接。

3.1.2 Layer Combination and Model Prediction

　　只有可训练的模型参数是在第 $0$ 层的嵌入，即所有用户的 $\mathbf{e}_{u}^{(0)}$ 和所有物品的 $\mathbf{e}_{i}^{(0)}$。当给出它们时，可以通过 $\text{Eq.3}$ 中定义的 LGC 来计算更高层的嵌入。在 $K$ 层 LGC 之后，我们进一步结合在每一层获得的嵌入，形成最终的用户和物品表示：

　　　　$\mathbf{e}_{u}=\sum\limits _{k=0}^{K} \alpha_{k} \mathbf{e}_{u}^{(k)} ; \quad \mathbf{e}_{i}=\sum\limits _{k=0}^{K} \alpha_{k} \mathbf{e}_{i}^{(k)} \quad\quad\quad(4)$

　　其中，$\alpha_{k} \geq 0$ 表示第 $k$ 层嵌入在构成最终嵌入中的重要性。它可以被视为一个需要手动调整的超参数，也可以作为一个需要自动优化的模型参数。在实验中，发现将 $\alpha_{k}$ 均匀设置为 $1 /(K+1) $ 总体上具有良好的性能。

　　因此，我们不设计特殊的组件来优化 $\alpha_{k}$，以避免不必要地使 LightGCN 复杂化，并保持其简单性。我们执行图层组合来得到最终表示的原因有三方面。

• • 随着层数增加，将导致过平滑的问题，故不能简单使用最后一层的嵌入；　　
  • 不同层捕获了不同的语义信息；　　　　
  • 将不同层的嵌入加权和，可以捕获与图卷积自连接的效果；　　

　　模型预测被定义为用户和项目最终表示的内积：

　　　　$\hat{y}_{u i}=\mathbf{e}_{u}^{T} \mathbf{e}_{i}  \quad\quad\quad(5)$

3.1.3 Matrix Form

　　用户-物品交互矩阵（user-item interaction matrix）定义为：$\mathbf{R} \in \mathbb{R}^{M \times N}$，其中 $M$ 和 $N$ 分别代表着用户、物品的数量。如果 $R_{u i}= 1$ ，则说明用户 $u$ 和物品 $i$ 有交互，否则为 $0$。因此，得到用户-物品图（user-item graph）的邻接矩阵：

　　　　$\mathbf{A}=\left(\begin{array}{cc}\mathbf{0} & \mathbf{R} \\\mathbf{R}^{T} & \mathbf{0}\end{array}\right)   \quad\quad\quad(6)$

　　第 $0$ 层的嵌入矩阵 $\mathbf{E}^{(0)} \in \mathbb{R}^{(M+N) \times T}$，$T$ 代表着嵌入的维度，可以得到 LGC 的矩阵等价形式为：

　　　　$\mathbf{E}^{(k+1)}=\left(\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}\right) \mathbf{E}^{(k)} \quad\quad\quad(7)$

　　其中 $\mathbf{D}$ 是一个 $(M+N) \times(M+N)$ 对角矩阵，其中每个元 $D_{i i}$ 表示邻接矩阵 $A$ 的第 $i$ 行向量中的非零项的数目。最后，我们得到了用于模型预测的最终嵌入矩阵为：

　　　　$\begin{aligned}\mathbf{E} &=\alpha_{0} \mathbf{E}^{(0)}+\alpha_{1} \mathbf{E}^{(1)}+\alpha_{2} \mathbf{E}^{(2)}+\ldots+\alpha_{K} \mathbf{E}^{(K)} \\&=\alpha_{0} \mathbf{E}^{(0)}+\alpha_{1} \tilde{\mathbf{A}} \mathbf{E}^{(0)}+\alpha_{2} \tilde{\mathbf{A}}^{2} \mathbf{E}^{(0)}+\ldots+\alpha_{K} \tilde{\mathbf{A}}^{K} \mathbf{E}^{(0)}\end{aligned}  \quad\quad\quad(8)$

　　其中，$ \tilde{\mathbf{A}}=\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}$ 代表着对称标准化矩阵。

3.2 Model Analysis

3.2.1 Relation with SGCN

　　在[40]中，作者论证了GCN在节点分类中的不必要的复杂性，并提出了SGCN，它通过去除非线性并将多个权值矩阵压缩为一个权值矩阵来简化GCN。SGCN中的图卷积定义为：

　　　　$\mathbf{E}^{(k+1)}=(\mathbf{D}+\mathbf{I})^{-\frac{1}{2}}(\mathbf{A}+\mathbf{I})(\mathbf{D}+\mathbf{I})^{-\frac{1}{2}} \mathbf{E}^{(k)}  \quad\quad\quad(9)$

　　其中，$\mathbf{I} \in \mathbb{R}^{(M+N) \times(M+N)}$ 是一个单位矩阵，它被添加在 $A$ 上以包含自连接。在接下来的分析中，为了简单起见，我们省略了 $ (\mathbf{D}+\mathbf{I})^{-\frac{1}{2}} $ 项，因为它只重新缩放嵌入。在SGCN中，在最后一层获得的嵌入用于下游预测任务，可以表示为：【牛顿二项展开式】

　　　　$\begin{aligned}\mathbf{E}^{(K)} &=(\mathbf{A}+\mathbf{I}) \mathbf{E}^{(K-1)}=(\mathbf{A}+\mathbf{I})^{K} \mathbf{E}^{(0)} \\&=\left(\begin{array}{c}K \\0\end{array}\right) \mathbf{E}^{(0)}+\left(\begin{array}{c}K \\1\end{array}\right) \mathbf{A} \mathbf{E}^{(0)}+\left(\begin{array}{c}K \\2\end{array}\right) \mathbf{A}^{2} \mathbf{E}^{(0)}+\ldots+\left(\begin{array}{c}K \\K\end{array}\right) \mathbf{A}^{K \mathbf{E}^{(0)}}\end{aligned}    \quad\quad\quad(10)$

　　上述推导表明，在 $A$ 中插入自连接并在其上传播嵌入，本质上等同于在每个LGC层上传播的嵌入的加权和。

3.2.2 Relation with APPNP

　　在工作[24]中，作者将 GCN 与Personalized PageRank[15] 联系起来，提出了一种名为 APPNP 的 GCN 变体，它可以远程传播而不会有过度平滑的风险。受个性化 PageRank 中的传送设计的启发，APPNP 补充了每个传播层的起始特征（即第 $0$ 层嵌入），这可以平衡保持局部性的需要（即保持靠近根节点以缓解过度平滑）和利用来自一个大邻域的信息。在APPNP中的传播层被定义为：

　　　　$\mathbf{E}^{(k+1)}=\beta \mathbf{E}^{(0)}+(1-\beta) \tilde{\mathbf{A}} \mathbf{E}^{(k)}   \quad\quad\quad(11)$

　　其中 $\beta$ 是控制传播中控制起始特征保留的传送概率。$\tilde{\mathbf{A}} $ 为归一化邻接矩阵。在APPNP中，最后一层用于最终的预测，即：

　　　　$\begin{aligned}\mathbf{E}^{(K)} &=\beta \mathbf{E}^{(0)}+(1-\beta) \tilde{\mathbf{A}} \mathbf{E}^{(K-1)} \\&=\beta \mathbf{E}^{(0)}+\beta(1-\beta) \tilde{\mathbf{A}} \mathbf{E}^{(0)}+(1-\beta)^{2} \tilde{\mathbf{A}}^{2} \mathbf{E}^{(K-2)} \\&=\beta \mathbf{E}^{(0)}+\beta(1-\beta) \tilde{\mathbf{A}} \mathbf{E}^{(0)}+\beta(1-\beta)^{2} \tilde{\mathbf{A}}^{2} \mathbf{E}^{(0)}+\ldots+(1-\beta)^{K} \tilde{\mathbf{A}}^{K} \mathbf{E}^{(0)}\end{aligned}   \quad\quad\quad(12)$

　　结合 $\text{Eq.8}$，我们可以看到，通过相应地设置 $\alpha_{k}$，LightGCN可以完全恢复APPNP使用的预测嵌入。因此，LightGCN共享了APPNP在对抗过平滑方面的优势——通过正确地设置 $\alpha$，我们允许使用一个大的 $K$ 来进行具有可控过平滑的远程建模。另一个小的区别是，APPNP将自连接添加到邻接矩阵中。然而，正如我们之前所展示的，由于不同层的加权和，这是多余的。

3.2.3 Second-Order Embedding Smoothness

　　由于LightGCN 的线性性质，我们可以更深入地了解它是如何平滑嵌入的。在这里，我们分析了一个 $2$ 层的 LightGCN 来证明其合理性。以用户方面为例，直观地说，二阶平滑在交互物品上有重叠的用户。更具体地说，我们有：

　　　　$\mathbf{e}_{u}^{(2)}=\sum\limits _{i \in \mathcal{N}_{u}} \frac{1}{\sqrt{\left|\mathcal{N}_{u}\right|} \sqrt{\left|\mathcal{N}_{i}\right|}} \mathbf{e}_{i}^{(1)}=\sum\limits _{i \in \mathcal{N}_{u}} \frac{1}{\left|\mathcal{N}_{i}\right|} \sum\limits _{v \in \mathcal{N}_{i}} \frac{1}{\sqrt{\left|\mathcal{N}_{u}\right|} \sqrt{\left|\mathcal{N}_{v}\right|}} \mathbf{e}_{v}^{(0)}     \quad\quad\quad(13)$

　　我们可以看到，如果另一个用户 $v$ 与目标用户 $u$ 有协同交互，那么 $v$ 在 $u$ 上的平滑强度可以用系数（否则为0）来衡量：

　　　　$c_{v->u}=\frac{1}{\sqrt{\left|\mathcal{N}_{u}\right|} \sqrt{\left|\mathcal{N}_{v}\right|}} \sum\limits _{i \in \mathcal{N}_{u} \cap \mathcal{N}_{v}} \frac{1}{\left|\mathcal{N}_{i}\right|}    \quad\quad\quad(14)$

　　这个系数是相当可解释的：二阶邻域 $v$ 对 $u$ 的影响由 1)共交互物品的数量越多越大；2)共互动物品的受欢迎程度越低（即用户个性化偏好越明显）越大；3) $v$ 的活动越少，越活跃越大。这种可解释性很好地满足了CF在测量用户相似度时的假设，并证明了LightGCN的合理性。

3.3 Model Training

　　LightGCN的可训练参数只是第 $0$ 层的嵌入 $\Theta=\left\{\mathbf{E}^{(0)}\right\}$。我们采用 Bayesian Personalized Ranking (BPR)损失，一种成对的损失，鼓励对观察到的条目的预测高于未观察到的对应项：

　　　　$L_{B P R}=-\sum\limits _{u=1}^{M} \sum\limits _{i \in \mathcal{N}_{u}} \sum\limits _{j \notin \mathcal{N}_{u}} \ln \sigma\left(\hat{y}_{u i}-\hat{y}_{u j}\right)+\lambda\left\|\mathbf{E}^{(0)}\right\|^{2}    \quad\quad\quad(15)$

4 Experiments

数据集

　　

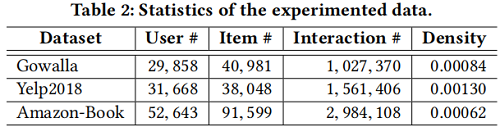
对比实验

　　

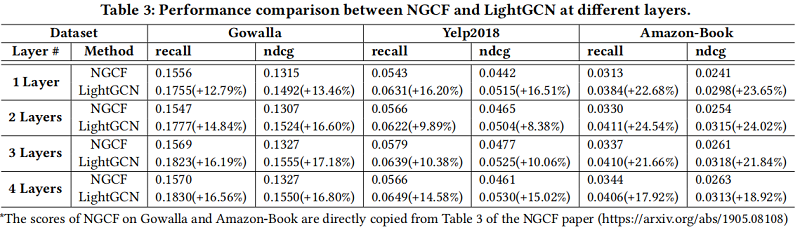
5 Conclusion

　　在这项工作中，我们提出了不必要的复杂设计，并进行了实证研究来证明这一论点。我们提出了LightGCN，它由两个基本组件组成：光图卷积和层组合。在光图卷积中，我们放弃了特征变换和非线性激活——GCN 中的两种标准操作，但不可避免地增加了训练的难度。在层组合中，我们将一个节点的最终嵌入作为其嵌入对所有层的加权和，证明了它包含了自连接的影响，有助于控制过平滑。我们进行了实验来证明LightGCN在简单方面的优点：更容易被训练，更好的泛化能力，更有效。