Popular generalized linear models|GLMM| Zero-truncated Models|Zero-Inflated Models|matched case–control studies|多重logistics回归|ordered logistics regression

==============================================================

Popular generalized linear models

将不同类型的数据做数值转换，转换为线性模型。

连续型变量且正态分布选择

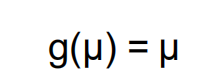
离散型变量且二项分布选择logistics

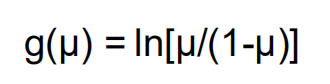
计数变量且负二项分布选择自然对数

負二項分布是統計學上一種描述在一系列独立同分布的伯努利试验中，失败次数到达指定次数（记为r）时成功次数的離散概率分布。 比如，如果我们定义掷骰子随机变量x值为x=1时为失败，所有x≠1为成功，这时我们反复掷骰子直到1出现3次（失败次数r=3），此时非1数字出现次数的概率分布即为负二项分布。

计数变量且负泊松分布选择自然对数

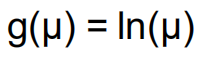
如果y值非常稀疏，则使用泊松回归。

过度离散，用负二项分布矫正。

得到原始数据先用K-S检验，考查是否符合泊松分布。

第二类错误计算方法是先计算power值，后根据1-power=第二类错误，得到第二类错误。

========================================================================

Generalized linear mixed models混合效应模型GLMM

空间自相关是指sample距离过近影响独立性。使用半方差图判断空间自相关：eg：

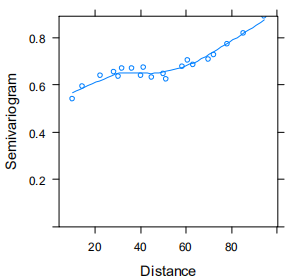
如果不使用半方差图，则需要去掉距离过近的sample。

Zero-truncated Models指没有数值为0 的变量值，比如医院人数，但是泊松分布还是会考虑变量为零时的概率值，这不符合客观规律，所以扩大已知项的概率，即Zero-truncated GLM。Eg：理论上值为零占总数据的20%，有数值的概率是80%，将所以实际数值对应概率除以80%，放大即可。

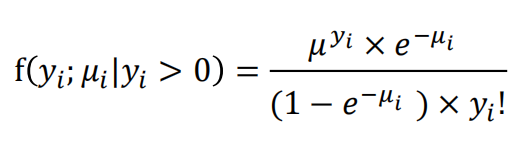
Zero-Inflated Models指变量数值为零的个数超过预期，比较贴近实际情况。我们将数据分成两个虚拟组；第一组仅包含零（假零）。该组也称为零质量的观测值。第二组是计数数据，可以生成零(真零)以及大于零的值。

有假零的概率如下：

====================================================================

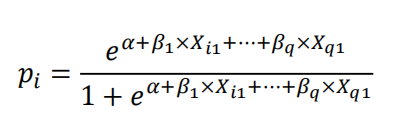
matched case–control studies

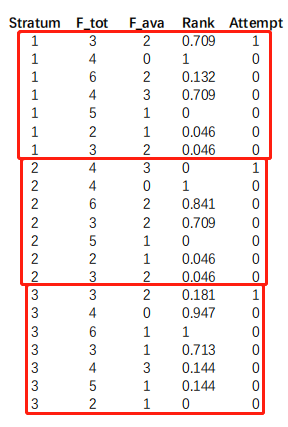
Eg :应该按照同一年来计算，即相同stratum取值内部，解释attempt取1或0.

=============================================================

多重logistics回归

多重logistics回归是分析样本的某些因素对另一个因素造成影响，与多元判别相同功能，即最终结果是分超过两类。

Rationale就是计算得到某y值的概率，比如汽车数据中得到gear=3时的概率。

Eg：汽车数据中用wt和cyl来解释gear，即计算gear=3、4、5的可能性

============================================================

ordered logistics regression

如果有顺序用ordered logistics regression

Complete separation如果数据过于理想在，而找不到合适β值

eg：x小相对应y小项，x大项对应y大项。，此情况找不对应β值。