Re：prime 关于质数的算法

Re：prime 关于质数的所有算法

绪言

所有代码若无说明，均采用快读模板

关于质数，无非就两大类：

1. 判断一个数字是不是质数
2. 找出[1,n]中所有的质数

先讲1：

Judge

判断x是不是质数

根据质数的定义，我们可以枚举所有小于x，大于1的正整数i。如果x%i==0，即i是x的因数，则x不是质数。

很明显，一个质数的因数是成对出现，且分别在sqrt(x)的两边。所以只要枚举到sqrt(x)即可。

bool judge(LL & x)
{
    if(x<2) return 0;
    LL sq=sqrt(x);
    for(re LL i=2;i<=sq;i++)
    {
        if(!(x%i)) return 0;
    }
    return 1;
}

时间复杂度O(sqrt(n))

那么，这里插一句嘴——只要再从1~n枚举一个数，不就可以得出1~n中所有的质数了嘛？！

(另外一种判断质数的方法等会再讲)

n=1.5*10^6

上面是指极限下1s能过的数据

bool judge(LL & x)//n=1.5*10^6 这里用IL反而会慢0.01s
{
    if(x<2) return 0;
    LL sq=sqrt(x);
    for(re LL i=2;i<=sq;i++)
    {
        if(!(x%i)) return 0;
    }
    return 1;
}
LL n;
int main()
{
    freopen("prime.in","r",stdin);
    freopen("nsqrtn.out","w",stdout);
    n=read();
    for(re LL i=1;i<=n;i++)
    {
        if(judge(i)) write(i);
    }
    return 0;
}

时间复杂度O(nsqrt(n))

n=4*10^6

这里只要把上面的那个n=1.5*10^6做一个小小的优化（可以理解为记忆化）

其实，我们在尝试枚举因数的时候，我们可以只要枚举质因数就好。

比如x=91

如果我枚举到i=2（某个质数）发现不能整除，那么91当然也不能被2的倍数（质数的（2倍以上的）倍数是不是质数）整除啊

所以，judge()中的枚举i只需要枚举1~sqrt(x)中的质数即可。

使用一个数组存储所有的质数吧。

LL his[1000000];
LL size;
bool judge(LL & x)//n=4*10^6
{
    if(x<2) return 0;
    LL sq=sqrt(x);
    for(re LL i=0;his[i]<=sq&&i<size;i++)
    {
        if(!(x%his[i])) return 0;
    }
    return 1;
}
LL n;
int main()
{
    freopen("prime.in","r",stdin);
    freopen("nsqrtnpro.out","w",stdout);
    n=read();
    his[size++]=2;
    if(n>=2) write(2);
    for(re LL i=3;i<=n;i++)
    {
        if(judge(i)) write(i),his[size++]=i;
    }
    return 0;
}

时间复杂度O(?)

接下来在看看

n=3*10^7

这次是埃氏筛（埃拉托斯特尼筛法）。

每找到一个质数，就将它的倍数打上标记即可。

如果循环到某个数的时候，它没有被打上标记

那么它就一定是质数了，

就再拿它去更新它的倍数。

bool book[30000000];
LL prime[30000000];
LL size;
LL n;
int main()//n=3*10^7
{
    freopen("prime.in","r",stdin);
    freopen("Eratosthenes.out","w",stdout);
    n=read();
    book[1]=1;
    prime[size++]=2;
    for(re LL i=2;i<=n;i++)
    {
        if(!book[i])
        {
            prime[size++]=i;
            write(i);
            for(re LL j=2;i*j<=n;j++)
            {
                book[i*j]=1;
            }
        }
    }
    return 0;
}

时间复杂度O(nloglogn)，已经非常接近于线性的了

（注意，虽然它的图像在10000以内的斜率看似比y=x还要小，但是我们比较的是其增长性，即：nloglogn的导数是单调递增的）

可能一阶导看不出来

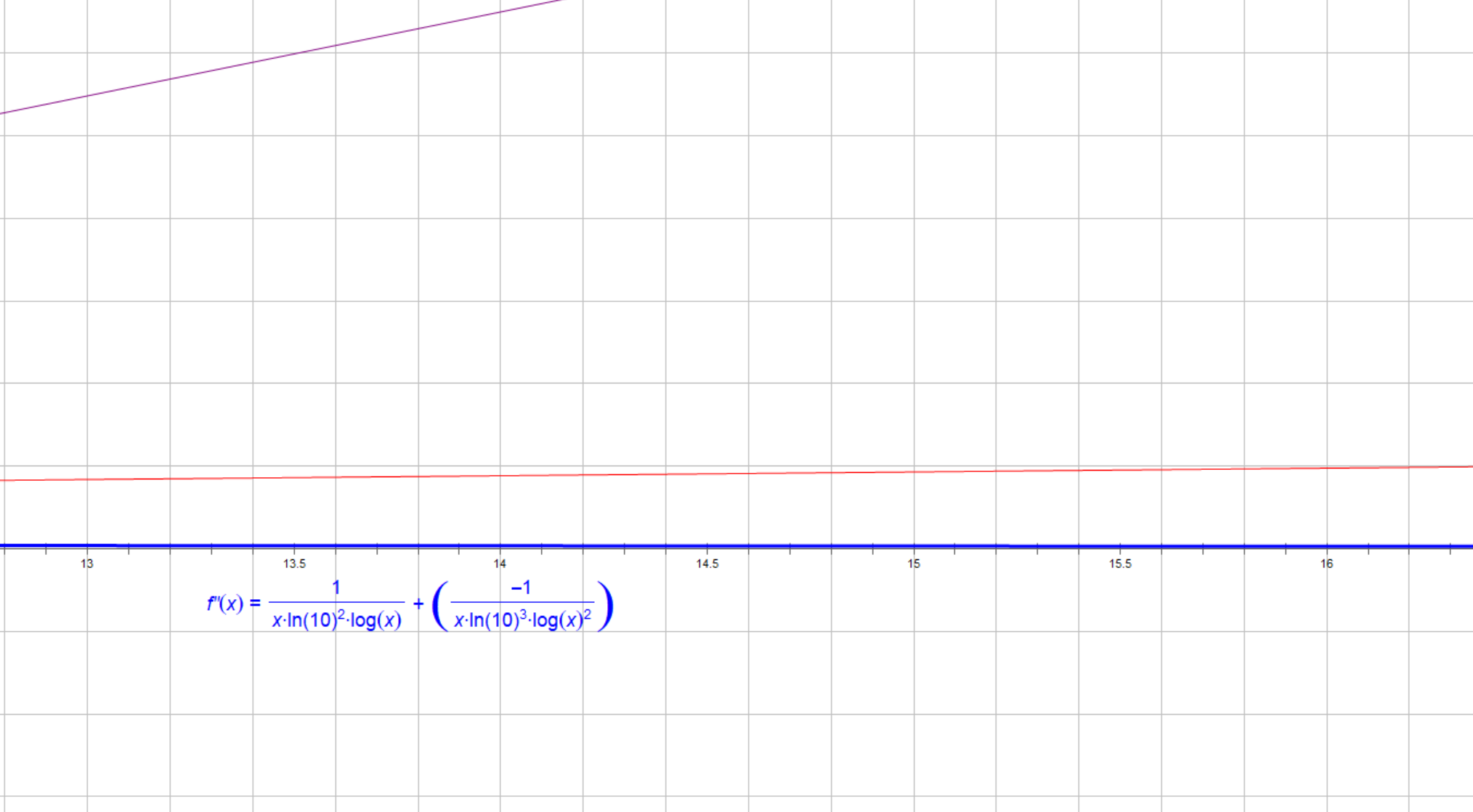
紫色：nloglogn

红色：f'(x)

蓝色：f''(x)

好了，不管那么多了，再看这次最强的筛法：欧拉筛 吧

n=3*10^7(***)

请先思考一下

为什么埃氏筛会超过线性呢？

因为其实，一个合数可能会被打上多次的合数标记

比如，枚举到2是质数的时候，会把4、6、8、10……打上标记

枚举到3是质数的时候，会把6、9、12……打上标记

然后6就被打了两次标记。

有一个更加严重的例子，一些合数甚至被打了很多次，这就浪费了很多次的机会，比如60

60这个数字被它的质因数们：2、3、5打了标记

而510510被它的质因数们：2、3、5、7、11、13、17打了标记。。。

浪费的时间就在这里了。。。

那么，欧拉筛：

#define MAXN 50000000
LL prime[MAXN];
bool book[MAXN];
LL n,size;
int main()
{
    freopen("prime.in","r",stdin);
    freopen("Euler.out","w",stdout);
    n=read();
    prime[size++]=2;
    book[1]=1;
    for(re LL i=2;i<=n;i++)
    {
        if(!book[i]) prime[size++]=i,write(i);
        for(re LL j=0;j<size&&i*prime[j]<=n;j++)
        {
            book[i*prime[j]]=1;
            if(i%prime[j]==0) break;
        }
    }
    return 0;
}

一样的套路。

首先一定要记忆化（保存prime数组）

其次无论当前的数是不是质数都要用这个数字i向后筛

但是仅仅筛到i%prime[j]==0，即i可以被从小到大的某个质数整除为止。

所以，对于一个i，第二层for仅仅会筛到它的最小质因数倍的i

即比如i=5，就只会筛走2*5，3*5，5*5（然后5%5==0 -> break;）

所以每个数只会被它的最小质因数筛——只会被筛一遍

所以它的时间复杂度是O(n)的

如果你还是不信：

#define MAXN 50000000
LL prime[MAXN];
bool book[MAXN];
LL n,size;
int main()
{
//    freopen("prime.in","r",stdin);
//    freopen("Euler.out","w",stdout);
    n=read();
    prime[size++]=2;
    book[1]=1;
    for(re LL i=2;i<=n;i++)
    {
        if(!book[i]) prime[size++]=i,write(i);
        for(re LL j=0;j<size&&i*prime[j]<=n;j++)
        {
            book[i*prime[j]]=1;
            cout<<i<<" "<<i*prime[j]<<endl;
            if(i%prime[j]==0) break;
        }
    }
    return 0;
}

验证

被筛的数字是不会相同的。

咦？那这个算法1s极限怎么和高贵的埃氏筛相差无几（明明是根本一样好吧！）啊~

因为它有一定的常数（用到了取模），还一定要保存质数（这个影响不大）

但是，在更大的数据下，欧拉筛才能展现出其真正的魅力！

比如说这个数据：

200'000'000(2*10^8，两亿)

看上去就很不错

用埃氏筛来跑，需要3.682s左右

但是用欧拉筛，只需要2.943s左右！

（以上数据为无输出数据，且仅用于对比，无实际意义）

所以以后考试的时候还是打埃氏筛吧——又简单常数又小！

最后——

Miller·Rabin

快速的大质数判断，基于随机算法。

可以在O(klogn)内判断一个数字是不是质数，其中k为判断的次数（稍后你就懂了），n是这个数字的大小。

我不太懂它的证明过程，但是我觉得我这么菜，只要会用就好了……

以下是步骤：

1. f是一个小质数，a是要测试的数字，d=a-1
2. 去除d的因数2（即把d除以二直到d变成奇数）
3. 计算t=f^d%a(快速幂)
4. 循环{d/=2;t*=t;t%a;}直到d=a-1或t=1或t=a-1
5. 这时如果t==a-1或者d是奇数，那么可以粗劣地判断a是质数
6. 多选几个f判断，同时满足的话，就可以说是质数了