51Nod1518 稳定多米诺覆盖 动态规划 插头dp 容斥原理

原文链接https://www.cnblogs.com/zhouzhendong/p/51Nod1518.html

题目传送门 - 51Nod1518

题意

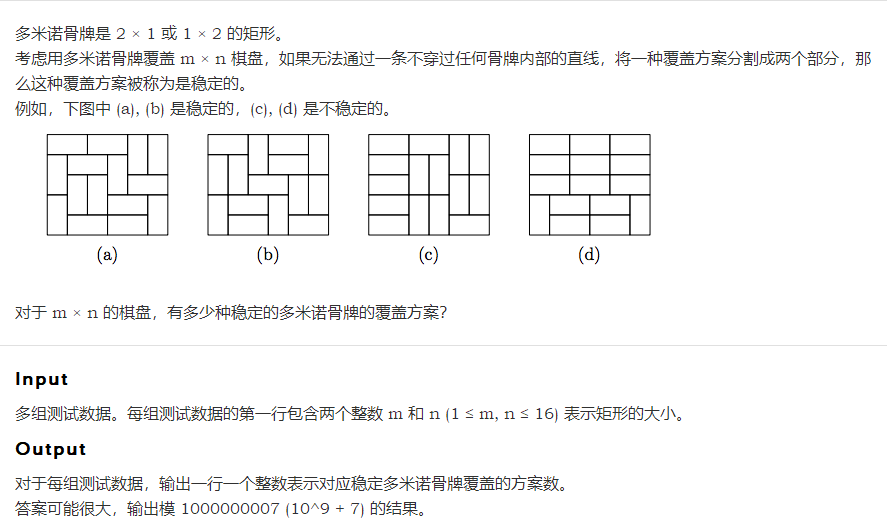
51Nod真是个好OJ ，题意概括的真好，有助于博主偷懒不写题意概括。给51Nod 点赞！

题解

　　首先，我们忽略那个“稳定”的要求，求方案数。

　　显然是一个插头dp裸题，我们可以在 $O(n^2\cdot 2^n)$ 的时间复杂度中求出所有长宽的矩形区域的覆盖方案数。

　　然后我们考虑容斥原理，奇加偶减。首先，枚举哪些相邻行之间有一条不穿过骨牌的直线，然后，用一个 $O(n)$ DP 来解决相邻列之间分割线的容斥。

　　总的时间复杂度 $O(n^22^n)$ 。打出表之后，询问 $O(1)$ 。

代码

看着那些运行效率榜上15MS的代码我于是交了一份 0MS 的代码。正常的代码在这份代码之后。

#include <bits/stdc++.h>
int n,m,ans[17][17]={
{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
{0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
{0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,6,0,108,0,1182,0,10338,0,79818,0,570342},
{0,0,0,0,0,6,0,124,62,1646,1630,18120,25654,180288,317338,1684956,3416994},
{0,0,0,0,0,0,124,0,13514,0,765182,0,32046702,0,136189727,0,378354090},
{0,0,0,0,0,108,62,13514,25506,991186,3103578,57718190,238225406,965022920,388537910,937145938,315565230},
{0,0,0,0,0,0,1646,0,991186,0,262834138,0,462717719,0,560132342,0,699538539},
{0,0,0,0,0,1182,1630,765182,3103578,262834138,759280991,264577134,712492587,886997066,577689269,510014880,807555438},
{0,0,0,0,0,0,18120,0,57718190,0,264577134,0,759141342,0,567660301,0,47051173},
{0,0,0,0,0,10338,25654,32046702,238225406,462717719,712492587,759141342,398579168,83006813,821419653,942235780,558077885},
{0,0,0,0,0,0,180288,0,965022920,0,886997066,0,83006813,0,690415372,0,620388364},
{0,0,0,0,0,79818,317338,136189727,388537910,560132342,577689269,567660301,821419653,690415372,796514774,696587391,175421667},
{0,0,0,0,0,0,1684956,0,937145938,0,510014880,0,942235780,0,696587391,0,856463275},
{0,0,0,0,0,570342,3416994,378354090,315565230,699538539,807555438,47051173,558077885,620388364,175421667,856463275,341279366}
};
int main(){
	while (~scanf("%d%d",&n,&m))
		printf("%d\n",ans[n][m]);
	return 0;
}

　　

正常的代码

#include <bits/stdc++.h>
using namespace std;
int read(){
	int x=0;
	char ch=getchar();
	while (!isdigit(ch))
		ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+ch-48,ch=getchar();
	return x;
}
const int N=17,S=1<<16,mod=1e9+7;
int n,m,dp[2][S],tot[N][N],ans[N][N];
int gbit(int v,int d){
	return (v>>(d-1))&1;
}
void Solve_tot(int n,int m){
	memset(dp,0,sizeof dp);
	int T0=1,T1=0;
	dp[T1][(1<<m)-1]=1;
	for (int i=1;i<=n;i++){
		for (int j=1;j<=m;j++){
			T0^=1,T1^=1;
			memset(dp[T1],0,sizeof dp[T1]);
			for (int s=0;s<(1<<m);s++){
				int v=dp[T0][s];
				if (!v)
					continue;
				dp[T1][s^(1<<(j-1))]=(dp[T1][s^(1<<(j-1))]+v)%mod;
				if (j>1&&!gbit(s,j-1)&&gbit(s,j)){
					int _s=s^(1<<(j-2));
					dp[T1][_s]=(dp[T1][_s]+v)%mod;
				}
			}
		}
		tot[i][m]=dp[T1][(1<<m)-1];
	}
}
void Get_tot(int n){
	for (int m=1;m<=16;m++)
		Solve_tot(n,m);
}
int GetV(int n,int s,int len){
	int v=1;
	for (int i=1,j;i<=n;i=j){
		for (j=i;j<n&&!((s>>j)&1);j++);
		j++;
		v=1LL*v*tot[j-i][len]%mod;
	}
	return v;
}
int cnt_1(int v){
	int ans=0;
	while (v)
		ans+=v&1,v>>=1;
	return ans;
}
void Solve_ans(int n,int m){
	int dp[N],v[N];
	for (int s=0;s<(1<<n);s++){
		if (!(s&1))
			continue;
		memset(dp,0,sizeof dp);
		for (int i=1;i<=m;i++)
			v[i]=GetV(n,s,i);
		dp[0]=1;
		for (int i=1;i<=m;i++)
			for (int j=0;j<i;j++)
				dp[i]=(-1LL*dp[j]*v[i-j]+dp[i])%mod;
		int f=(cnt_1(s)&1)?-1:1;
		for (int i=1;i<=m;i++)
			ans[n][i]=(ans[n][i]+f*dp[i])%mod;
	}
}
void Get_ans(int m){
	memset(ans,0,sizeof ans);
	for (int n=1;n<=16;n++)
		Solve_ans(n,m);
	for (int i=1;i<=m;i++)
		for (int j=1;j<=m;j++)
			ans[i][j]=(ans[i][j]+mod)%mod;
}
int main(){
	Get_tot(16);
	Get_ans(16);
	while (~scanf("%d%d",&n,&m))
		printf("%d\n",ans[n][m]);
	return 0;
}