[Arc063F] Snuke's Coloring 2

[Arc063F] Snuke's Coloring 2

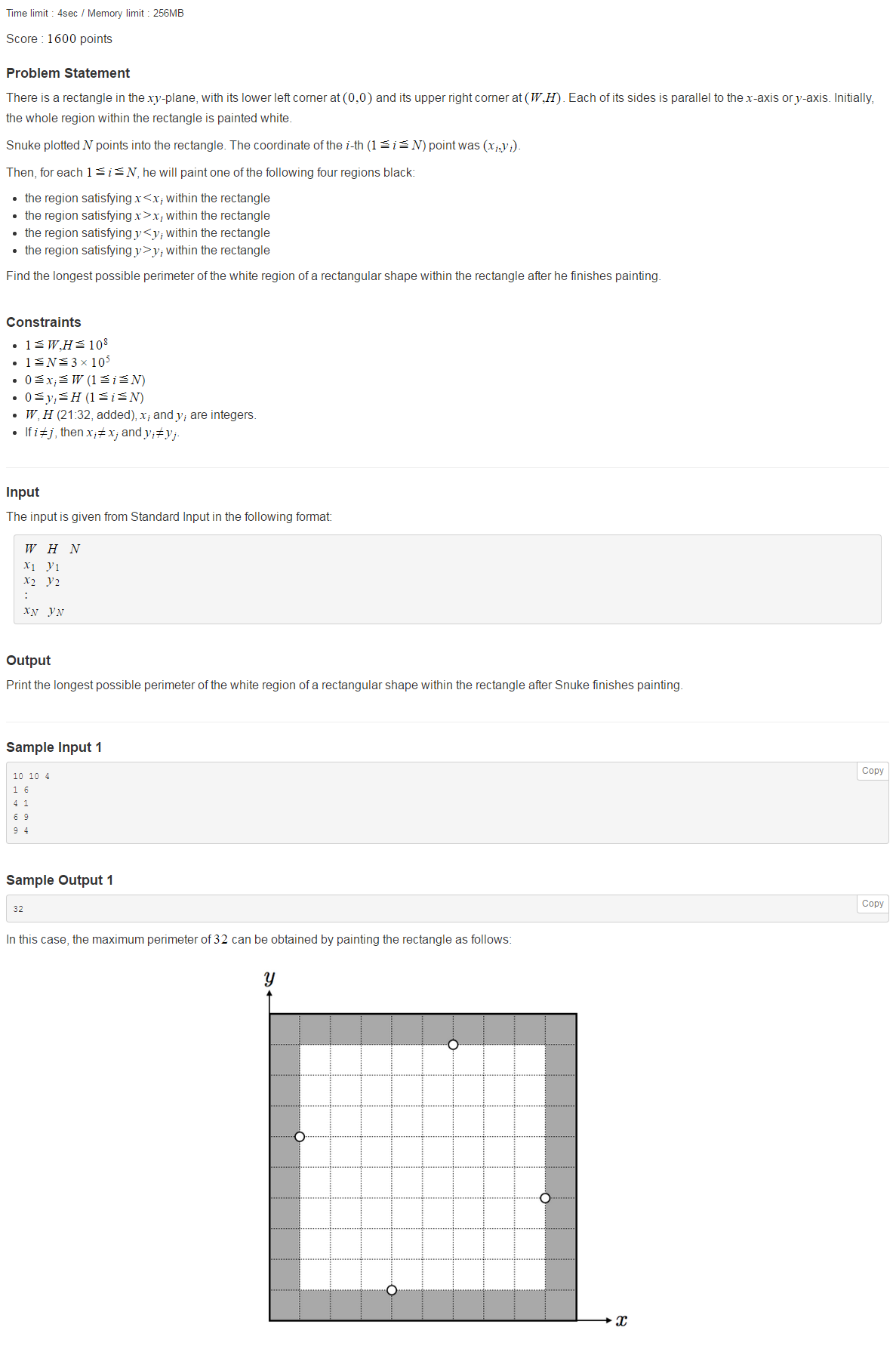
题目大意

给你一个网格图，一些点上有标记，求边长最大空白矩形。

试题分析

专门卡\(\log^2 n\)系列。

首先由题意我们可以找到答案的下界：\(\min(H,W)\times 2+2\)。

那么就是说这个矩形的周长如果要大于下界肯定会跨越中轴线\(H\)或\(W\)，那么我们只需要在两边枚举即可。

这个东西看起来没什么用，我们姑且将其当作常数优化，但是在后面的讨论中它极大地简化了问题。

继续考虑传统扫描线的方向，那么看看当我们确定了任意一个边界的时候可以干什么。

假定这里枚举的是右边界，然后左边界又没有东西可以维护了，那就直接让线段树维护：枚举右边界到点\(i\)，左边界为下标时的周长最大值。

现在就是扫描线的问题了，既然维护的是右边界和左边界，那么就肯定按照x轴从左向右扫。

对于上下界的部分，对于每个点维护两个单调栈，方向如下图。

但是这样一来的话就需要开主席树模拟单调栈，相当恶心，并且多了一个log。

怎么办呢？上面我们说过，这个矩形肯定会跨越中轴线，也就是说，我们只需要在中轴线上面维护一个，在下面维护一个单调栈就足够了。

于是，我们的矩形变成了这个样子：

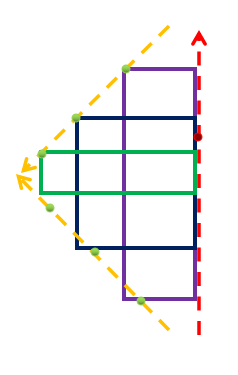
那么下面就是考虑在单调栈进出的时候去更新线段树了，这里建议画一下图：

• 我们枚举点并加入左边界的考虑部分，因为这个点相对于上一个点会向上移动，加入这个点的时候首先需要弹掉单调队列在它下面的点，然后要把编号在\({id_{stack_{top}}}\)和\({id_{stack_{last\space top}}}\)之间的这些点都减去\(y_i-y_{id_{stack_{top}}}\)，因为需要将当前右边界转到下一个点上去。
• 对于上面也是相同，只需要维护一个如图反着的单调队列即可。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<algorithm>
//#include<ctime>
//#include<cmath>
//#include<queue>

using namespace std;
#define LL long long

inline LL read(){
	LL x=0,f=1; char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*f;
}
const LL INF = 2147483600;
const LL MAXN = 500010;

struct data{
	LL x,y;
}p[MAXN+1],a[MAXN+1],b[MAXN+1];
data make_data(LL xx,LL yy){
	data a; a.x=xx; a.y=yy; return a;
}
LL N,W,H;
LL tag[MAXN<<2],tr[MAXN<<2];
bool cmp(data a,data b){
	if(a.x!=b.x) return a.x<b.x;
	return a.y<b.y;
}
inline void tage_lazy(LL rt){
	if(!tag[rt]) return ;
	tag[rt<<1]+=tag[rt]; tag[rt<<1|1]+=tag[rt];
	tr[rt<<1]+=tag[rt]; tr[rt<<1|1]+=tag[rt];
	tag[rt]=0;
	return ;
}
inline void update(LL rt,LL l,LL r,LL L,LL R,LL k){
	if(L>R) return ;
	if(L<=l&&R>=r){tr[rt]+=k; tag[rt]+=k; return ;} tage_lazy(rt);
	LL mid=(l+r)>>1; if(L<=mid) update(rt<<1,l,mid,L,R,k);
	if(R>mid) update(rt<<1|1,mid+1,r,L,R,k);
	tr[rt]=max(tr[rt<<1],tr[rt<<1|1]); return ;
} LL ans=0;

inline void work(){
	sort(p+1,p+N+1,cmp);
	memset(tr,0,sizeof(tr));
	memset(tag,0,sizeof(tag));
	LL l=0,r=0;
	for(LL i=1;i<=N;i++){
		if(p[i].y<=(H>>1)){
			LL lat=i-1;
			while(l&&a[l].y<p[i].y){
				update(1,1,N,a[l].x,lat,a[l].y-p[i].y);
				lat=a[l].x-1; --l;
			} if(lat!=i-1){
				a[++l]=make_data(lat+1,p[i].y);
			}
		} else{
			LL lat=i-1;
			while(r&&b[r].y>p[i].y){
				update(1,1,N,b[r].x,lat,p[i].y-b[r].y);
				lat=b[r].x-1; --r;
			} if(lat!=i-1){
				b[++r]=make_data(lat+1,p[i].y);
			}
		} a[++l]=make_data(i,0);
		b[++r]=make_data(i,H); update(1,1,N,i,i,H-p[i].x);
		ans=max(ans,tr[1]+p[i+1].x);
	} return ;
}

int main(){
	//freopen("a.in","r",stdin);
	//freopen(".out","w",stdout);
	W=read(),H=read(); N=read();
	for(LL i=1;i<=N;i++){
		p[i].x=read(),p[i].y=read();
	} p[++N].x=0; p[N].y=0; p[++N].x=W; p[N].y=H; work(); swap(W,H);
	for(LL i=1;i<=N;i++){
		swap(p[i].x,p[i].y);
	} work(); printf("%lld\n",ans*2);
	return 0;
}