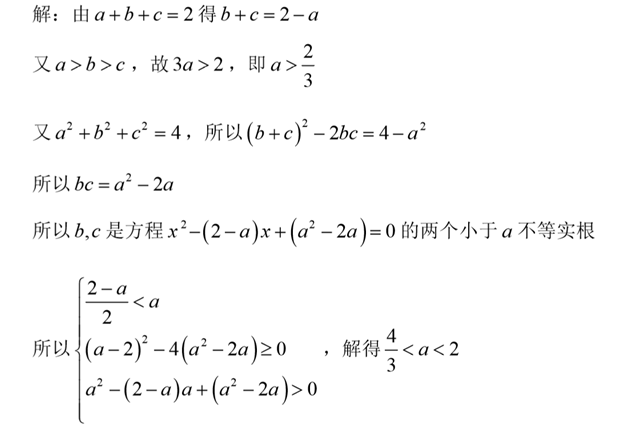
评：b+c,bc好比向量里的一组基底，可以将关于b,c的对称式表示出来.

MT【114】构造二次函数的更多相关文章

  1. MT【219】构造二次函数

    (2012北大保送)已知$f(x)$是二次函数,且$a,f(a),f(f(a)),f(f(f(a)))$是正项等比数列;求证:$f(a)=a$ 构造二次函数$f(x)=qx$,则$a,f(a),f(f ...

  2. MT【39】构造二次函数证明

    这种构造二次函数的方法最早接触的应该是在证明柯西不等式时: 再举一例: 最后再举个反向不等式的例子: 评:此类题目的证明是如何想到的呢?他们都有一个明显的特征$AB\ge(\le)C^2$,此时构造二 ...

  3. E - Rebuild UVALive - 7187 (二次函数极值问题)

    题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5531 Problem Description Archaeologists find ruins of ...

  4. Line Search and Quasi-Newton Methods 线性搜索与拟牛顿法

    Gradient Descent 机器学习中很多模型的参数估计都要用到优化算法,梯度下降是其中最简单也用得最多的优化算法之一.梯度下降(Gradient Descent)[3]也被称之为最快梯度(St ...

  5. Line Search and Quasi-Newton Methods

    Gradient Descent 机器学习中很多模型的参数估计都要用到优化算法,梯度下降是其中最简单也用得最多的优化算法之一.梯度下降(Gradient Descent)[3]也被称之为最快梯度(St ...

  6. 深入理解Plasma（四）Plasma Cash

    这一系列文章将围绕以太坊的二层扩容框架 Plasma,介绍其基本运行原理,具体操作细节,安全性讨论以及未来研究方向等.本篇文章主要介绍在 Plasma 框架下的项目 Plasma Cash. 在上一篇 ...

  7. [深入理解Android卷一全文-第七章]深入理解Audio系统

    由于<深入理解Android 卷一>和<深入理解Android卷二>不再出版,而知识的传播不应该由于纸质媒介的问题而中断,所以我将在CSDN博客中全文转发这两本书的全部内容. ...

  8. 一些有用的数学知识（Updating）

    文章目录 拉格朗日插值公式 微分中值定理 费马引理 拉格朗日中值定理 柯西中值定理 洛必达法则 连分数(NOI2021 D2T2 考点) 定义 结论 定理1 定理2 定理3 定理4 定理5 欧拉公式 ...

  9. MT【329】二次函数系数的最大最小

    已知二次函数$f(x)=ax^2+bx+c$有零点,且$a+b+c=1$ 若$t=\min\{a,b,c\}$求$t$的最大值. 分析:由$a,c$的对称性,不妨$c\ge a$即$2a+b\le1$ ...

随机推荐

  1. Qt-网易云音乐界面实现-9 照片墙功能

    最近车也买了,不过倒是没有想象的那么开心,车真的是想消耗品啊. 写这个专题了,本来是想好好的磨练一下自己,不过可能要在在理就GG了.腻味了. 还是先看下效果图吧 这个照片墙还差点东西,不过我个人认为需 ...

  2. TPO-21 C2 Which elective courses to take

    /* 加粗:语音部分 * 红色:单词部分 * 斜体:语法部分 * 下划线:信号词/句 */ 第 1 段 1.Listen to a conversation between a student and ...

  3. Python输出格式全总结

    输入输出 有几种方法可以显示程序的输出:数据可以以人类可读的形式打印出来,或者写入文件以供将来使用.本章将讨论一些可能性. 更漂亮的输出格式 到目前为止,我们遇到了两种写入值的方法:表达式语句 和 p ...

  4. canvas高效绘制10万图形,你必须知道的高效绘制技巧

    最近的一个客户项目中,简化的需求是绘制按照行列绘制很多个圆圈.需求看起来不难,上手就可以做,写两个for循环. 原始绘制方法 首先定义了很多Circle对象,在遍历循环中调用该对象的draw方法.代码 ...

  5. 【LeetCode算法题库】Day1：TwoSums & Add Two Numbers & Longest Substring Without Repeating Characters

    [Q1] Given an array of integers, return indices of the two numbers such that they add up to a specif ...

  6. DevOps on AWS之OpsWorks初体验

    AWS OpsWorks 是一款配置管理服务,提供 Chef 和 Puppet 的托管EC2虚拟机实例.Chef 和 Puppet 是自动化平台,允许用户使用代码来自动配置服务器.用户借助OpsWor ...

  7. Python交互数据库（Mysql | Mongodb | Redis）

    数据库 Mysql Mysql MySQL是一个关系型数据库管理系统,由瑞典MySQL AB公司开发,后来被Sun公司收购,Sun公司后来又被Oracle公司收购,目前属于Oracle旗下产品 MyS ...

  8. CentOs6.5中安装和配置vsftp简明教程[转]

    CentOs6.5中安装和配置vsftp简明教程 林涛 发表于:2017-3-17 10:10 分类:WebServer 标签: 101次 一.vsftp安装篇 复制代码代码如下: # 安装vsftp ...

  9. Scrum Meeting 10.23

    Scrum Meeting No.3 今天所完成的任务仍然停留在学习基础知识上.说实话,由于缺少安卓开发.web开发的经验,我们只能一步步摸索着来. 成员 已完成任务 下一阶段任务 徐越 阅读网上的博 ...

  10. 20162327WJH第二次实验——树

    20162327WJH第一次实验--线性结构 实 验 报 告 实 验 报 告 课程:程序设计与数据结构 班级: 1623 姓名: 王旌含 学号:20162327 成绩: 指导教师:娄嘉鹏 王志强 实验 ...