算法逆向6——RSA识别

本文原创作者：i春秋作家——icq5f7a075d

1. 算法介绍

RSA算法是一种用数论构造的、基于大合数因子分解困难性的公开密钥密码。由于RSA密码既可用于加密，又可用于数字签名，安全、易懂，因此RSA密码已成为目前应用最广泛的公开密钥密码。许多勒索软件就是使用RSA加密，在没有私钥的情况下很难恢复数据。
在正式介绍RSA加密算法前，我们还需要知道一些数论的概念：
（1）互素关系(互质关系)：如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互素关系(互质关系)；
（2）乘法逆元(模反元素)：如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1被n整除，或者说ab被n除的余数是1。这时，b就叫做a的乘法逆元(模反元素)。
（3）欧拉函数；任意给定正整数n，计算小于n的正整数中与n互质的数的数目的方式就叫做欧拉函数，以φ(n)表示。如果n是质数，则 φ(n)=n-1
，因为质数与小于它的每一个数，都构成互质关系。如果n可以分解成两个互质的整数之积，n = p1 × p2，则φ(n) =φ(p1p2)
= φ(p1)φ(p2)=(p1-1)*(p2-1)。
（4）欧拉定理：如果两个正整数a和n互质，则n的欧拉函数φ(n)可以让下面的等式成立：
a^φ(n)=1 (mod n)

有了以上数论的知识，我们就可以理解RSA加密算法了。

加密算法描述 ：

（1）密钥的产生
a.选两个保密的大素数（素数又称质数）p和q；
b.计算n=p*q，φ(n) =（p-1）（q-1）；
c.选一整数e，满足1<e<φ(n)，且φ(n)与e互质；
d.计算d，满足d*e=1 (mod φ(n))，即d是e在φ(n)下的乘法逆元，因e与φ(n)互素，由模运算可知，它的乘法逆元一定存在；
e.以{e,n}为公开钥，{d,n}为秘密钥；
（2）加密
加密时首先将明文比特串分组，使得每个分组对应的十进制数小于n，即分组长度小于log 2 n，然后对每个明文分组m，作加密运算：c=m^e mod n ；
（3）解密
对密文分组的解密运算为：m=c^d mod n ；

2. RSA24程序逆向

24指的是密钥长度。

2.1. 定位关键位置

数据验证的过程在sub_4029B0中进行，也是RSA计算的过程。

2.2. Serial计算

小知识点：计算字符串长度：

cld
xor eax，eax
or ecx,-0x1     ;ecx=0xFFFFFFFF
repne  scas  byte ptr es:[edi] ; [edi]=字符串
not ecx
dec ecx    ；计算出字符串长度

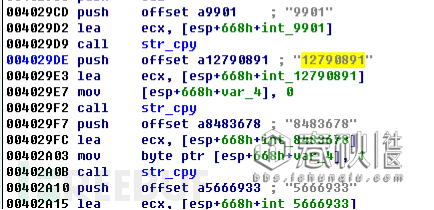
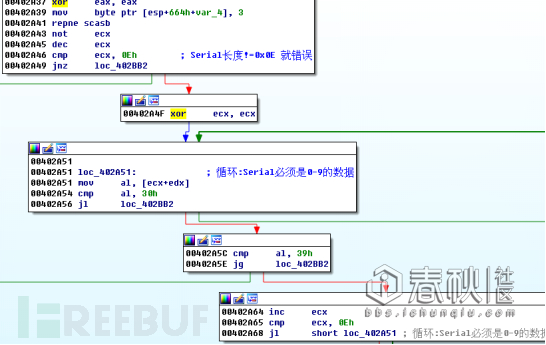
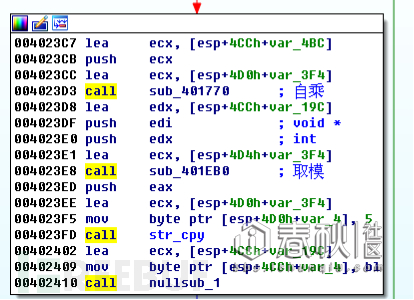
计算的过程可以用如下代码表示：
一个经典的 m e  mod n 算法：

m=7167622 #m的值不固定
n=12790891L
e=9901
c=1
while(e>0):
    if(e%2==0):
        e=e>>1
        m=(m*m)%n
    else:
        e=e-1
        c=(c*m)%n
print c

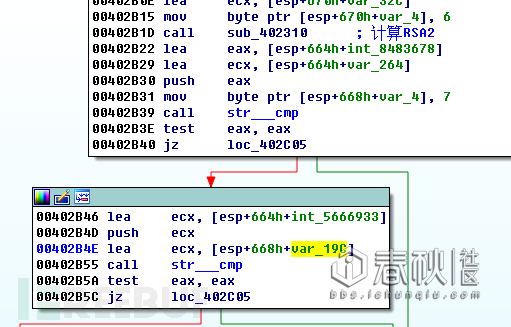
3. 总结

RSA的学习需要较高的理论基础，但是RSA实际上很简单，反汇编出的程序流程简单，很容易识别。

文末照例来点彩蛋：
① 在线分解质因数[/url] ：http://www.atool.org/quality_factor.php
②python中 的 gmpy2 模块。 
          gmpy2是Python的一个扩展库， 可以进行高精度运算，适用于 Miller-Rabin素数测试算法、大素数生成、欧几里德算法、求域中元素的逆、Jacobi符号、legendre符号等 。
RSA中经常进行 大素数 计算，gmpy2模块是一个不错的选择。
本次逆向程序中的n=12790891，e=9901，使用
在线分解质因数[/url] 工具，很容易计算出q=1667，p=7673，分解出借助 gmpy2 模块计算d，d=
gmpy2.invert(e, (p-1)*(q-1)) 。 q，p，n，d，e都有了，我们可以进行任意的RSA加密解密了。
注册机：

import gmpy2
n=12790891L
e=9901
c1=8483678
c2=5666933
q=1667
p=7673
d=gmpy2.invert(e, (p-1)*(q-1))
m1=pow(c1,d,n)
m2=pow(c2,d,n)
print m1,m2

本文属i春秋原创奖励计划，未经许可禁止转载！

本文如果出现错误，欢迎指出，感激不尽！

本文中的所有程序请在虚拟机中运行。

参考资料：

《加密与解密实战攻略》

《应用密码学》 曹天杰著

http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html

算法逆向1——简单算法逆向

算法逆向2——CRC32识别

算法逆向3——MD5算法识别

算法逆向4——SHA-1识别

算法逆向5——Base64识别

>>>>>>《黑客入门必备技能》   带你入坑，和逗比表哥们一起聊聊黑客的事儿，他们说高精尖的技术比农药都好玩！