bzoj 3028: 食物 -- 母函数

3028: 食物

Time Limit: 3 Sec  Memory Limit: 128 MB

Description

明明这次又要出去旅游了，和上次不同的是，他这次要去宇宙探险！

我们暂且不讨论他有多么NC，他又幻想了他应该带一些什么东西。理所当然的，你当然要帮他计算携带N件物品的方案数。

他这次又准备带一些受欢迎的食物，如：蜜桃多啦，鸡块啦，承德汉堡等等

当然，他又有一些稀奇古怪的限制：

每种食物的限制如下：

       承德汉堡：偶数个

       可乐：0个或1个

            鸡腿：0个，1个或2个

            蜜桃多：奇数个

            鸡块：4的倍数个

            包子：0个，1个，2个或3个

       土豆片炒肉：不超过一个。

            面包：3的倍数个

 

 

 

注意，这里我们懒得考虑明明对于带的食物该怎么搭配着吃，也认为每种食物都是以‘个’为单位（反正是幻想嘛），只要总数加起来是N就算一种方案。因此，对于给出的N,你需要计算出方案数，并对10007取模。

 

Input

输入样例1

  1

输出样例1

  1

 

输入样例2

  5

输出样例2

  35

 数据范围

   对于40%的数据，1<=N<=100000;

   对于所有数据，1<=n<=10^500;

HINT

关于母函数，要膜拜一下百度百科，讲解的非常详细，在这里我就不赘述了  http://baike.baidu.com/link?url=ks_0J2hQkdV4Bx-3BHgEDyAL7WSJjHcW86sdmMPfZfvaljHA7_-0IQbXhcap6kdOLyYyO8Rn1amc6wgVvR9EZuJl56bOCKpCtVNim8e0ig9L6XpaS-y8wj-FfBnj_qeK

首先我们先求出每个东西的母函数

相乘，化简得

我们知道

　　　　　　

所以

　　　　　　

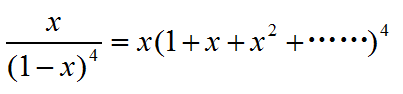
所以答案

　　　　　　

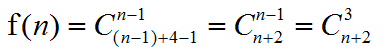
>_< 不知道为什么用 gets 输入就WA了。。

#include<cstdio>
#define P 10007
int n;char s[];
int main()
{
    scanf("%s",s+);
    for(int i=;s[i];i++)(n=(n<<)+(n<<)+(s[i]-''))%=P;
    printf("%d\n",n*(n+)%P*(n+)%P*%P);
}