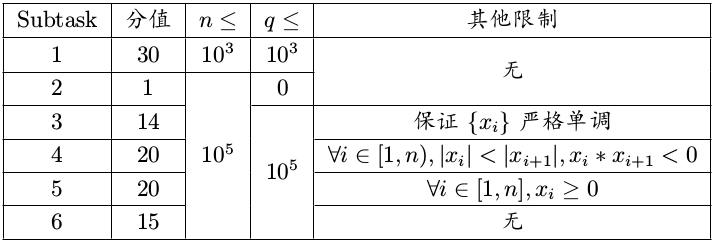
[CSP-S模拟测试]:z（模拟+map+小根堆）

题目背景

$\frac{1}{4}$遇到了一道水题，$eooooo$完全不会做，于是去请教小$D$。结果小$D$已经去了阿塞拜疆，于是，$\frac{1}{4}$只好来问你，这道题是这样的：

---

题目描述

在数轴上有一个线段，左端点在$0$，长度为$l$。
现在需要按顺序完成$n$个任务，第$i$个任务可以用$x_i$表示：当线段接触到点$x_i$时，视为完成任务，也就是$x_i$在线段某一端点上、或两端点之间。
你可以任意平移线段，求依次完成任务所需要的最短的平移总距离。
$q$次询问，每次给出一个$l$。

---

输入格式

从文件$z.in$中读入数据。
第一行，两个自然数$n,q$。
第二行，$n$个整数代表$x_i$。
第三行，$q$个自然数，代表询问的$l$。

---

输出格式

输出到文件$z.out$中。
输出$q$行，每行一个整数，代表对应询问的答案。

---

样例

样例输入1：

9 6
2 -3 -1 1 2 3 5 3 7
0 1 2 3 4 5

样例输出1：

21
16
11
10
9
8

样例输入2：

8 8
5 0 5 15 0 -10 0 -20
20 15 14 11 10 5 1 0

样例输出2：

20
20
22
28
30
50
74
80

---

数据范围与提示

样例$1$解释：

当$l=3$时：
一开始在$[0,3]$，完成任务$1$。
移动到$[−3,0]$，完成任务$2,3$。
移动到$[0,3]$，完成任务$4,5,6$。
移动到$[2,5]$，完成任务$7,8$。
移动到$[4,7]$，完成任务$9$。
$ans=3+3+2+2=10$。

数据范围：

保证$n,q\in [0,10^5],x_i\in [−10^9,10^9],l\in [0,10^9]$。

---

题解

首先，必须是挨个完成任务，所以如果有一个任务满足$x_{i-1}<x_i<x_{i+1}$或$x_{i-1}>x_i>x_{i+1}$，那么可以删去它。

这样的话，路径肯定是向前走再向后走，于是我们先假设$l=0$，那么答案会是一个一次函数。

那么接着考虑$l\neq 0$，如果$l$不超过最小的位移绝对值时，答案还是一个一次函数；如果超过了的话，我们可以将三个位移合并为一个即可。

将问题离线，利用$map$和$prority_queue$维护即可最小绝对值即可。

代码实现稍复杂u，调了好久……

时间复杂度：$\Theta(n\log n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int N,Q;
int x[100001];
pair<int,int> l[100001];
map<int,int> mp;
long long sum,ans[100001];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
long long calc(long long x)
{
	if(!mp.empty()&&mp.begin()->second<0)return sum-(mp.size()-1)*x;
	return sum-mp.size()*x;
}
int main()
{
	scanf("%d%d",&N,&Q);
	int lst=0;
	for(int i=1;i<=N;i++)
	{
		int a;scanf("%d",&a);
		if(a==lst)continue;
		if(x[0]&&((x[x[0]]<0&&a<lst)||(x[x[0]]>0&&a>lst)))x[x[0]]+=a-lst;
		else x[++x[0]]=a-lst;
		lst=a;
	}
	for(int i=1;i<=Q;i++)
	{
		scanf("%d",&l[i].first);
		l[i].second=i;
	}
	sort(l+1,l+Q+1);
	for(int i=1;i<=x[0];i++)
	{
		sum+=abs(x[i]);
		mp[i]=x[i];
		q.push(make_pair(abs(x[i]),i));
	}
	int t=1;
	while(!q.empty())
	{
		pair<int,int> flag=q.top();q.pop();
		auto _=mp.lower_bound(flag.second);
		pair<int,int> p=make_pair(_->first,_->second);
		if(_==mp.end()||p.first!=flag.second||abs(p.second)!=flag.first)continue;
		while(t<=Q&&abs(p.second)>l[t].first)ans[l[t].second]=calc(l[t++].first);
		auto begin=mp.begin();
		if(p!=make_pair(begin->first,begin->second))
		{
			auto endle=prev(mp.end());
			if(p!=make_pair(endle->first,endle->second))
			{
				auto pr=prev(_),nx=next(_);
				mp.erase(pr);mp.erase(nx);
				pair<int,int> pre=make_pair(pr->first,pr->second);
				pair<int,int> nxt=make_pair(nx->first,nx->second);
				flag.first=p.second;
				sum-=abs(p.second);
				flag.first+=pre.second;
				sum-=abs(pre.second);
				flag.first+=nxt.second;
				sum-=abs(nxt.second);
				_->second=flag.first;
				sum+=abs(flag.first);
				q.push(make_pair(abs(flag.first),flag.second));
			}
			else
			{
				sum-=abs(p.second);
				mp.erase(_);
			}
		}
		else
		{
			if(p.second>0)
			{
				auto endle=prev(mp.end());
				if(p!=make_pair(endle->first,endle->second))
				{
					auto nx=next(_);mp.erase(nx);
					pair<int,int> nxt=make_pair(nx->first,nx->second);
					flag.first=p.second;
					sum-=abs(p.second);
					flag.first+=nxt.second;
					sum-=abs(nxt.second);
					if(flag.first)
					{
						_->second=flag.first;
						sum+=abs(flag.first);
						q.push(make_pair(abs(flag.first),flag.second));
					}
					else mp.erase(_);
				}
				else
				{
					sum-=abs(p.second);
					mp.erase(_);
				}
			}
		}
	}
	while(t<=Q)ans[l[t].second]=calc(l[t++].first);
	for(int i=1;i<=Q;i++)printf("%lld\n",ans[i]);
	return 0;
}

---

rp++