力扣77(Java)-组合（中等）

题目：

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/combinations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

参考：代码随想录视频 & 代码随想录题解

回溯（递归） + 剪枝  注意：有回溯就会有递归

回溯可以想象成一棵树，集合的大小代表数的深度，递归的深度代表数的深度。

回溯三步曲：

1.确定回溯函数的参数及返回值

参数根据具体问题来补充，返回值一般为void

void backtracking(参数)

2.确定终止条件，终止条件一般都是找到叶子结点（具体问题具体分析）

if (终止条件){
    存放结果
    return;
}

3.遍历过程--单层递归逻辑

for （本层集合中的元素）{  //横向遍历
    处理当前结点；
    backtracking(路径，选择列表)； //纵向遍历
    回溯，撤销;

}

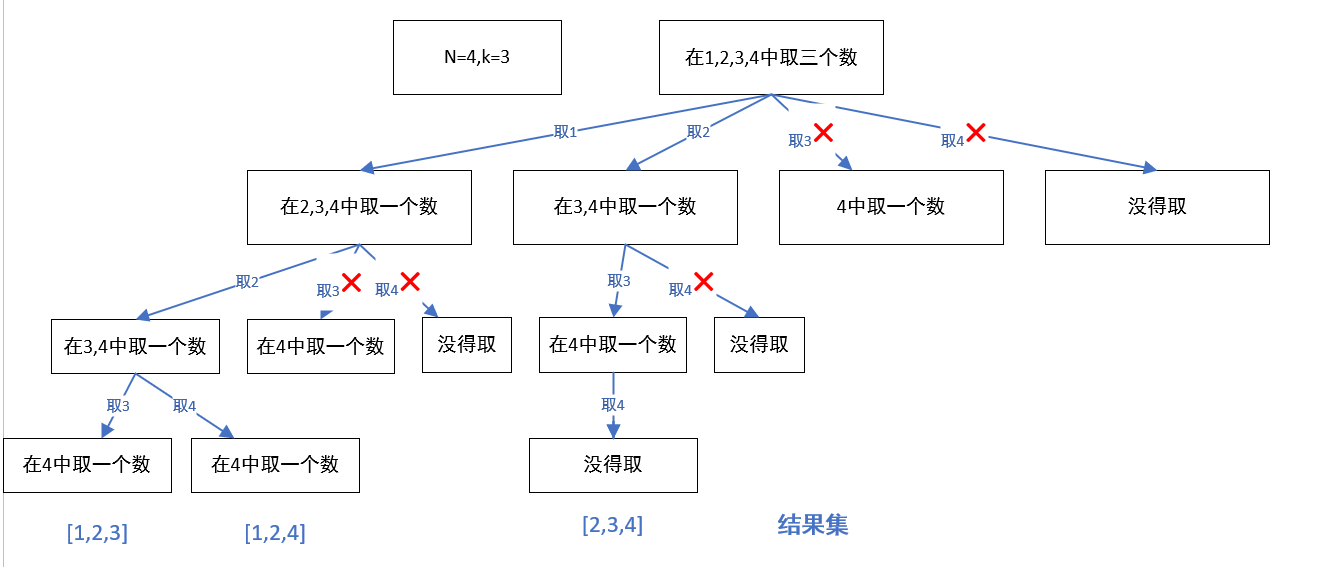
n相当于树的宽度，K相当于树的深度

思路：

1.定义两个全局遍历，一个temp用来存放符合条件的单一结果，一个result用来存放符合条件结果集合

2.递归的参数，一个为n，一个为k，还有一个startIndex代表下一层递归搜素的起始位置，为了防止取到重复组合

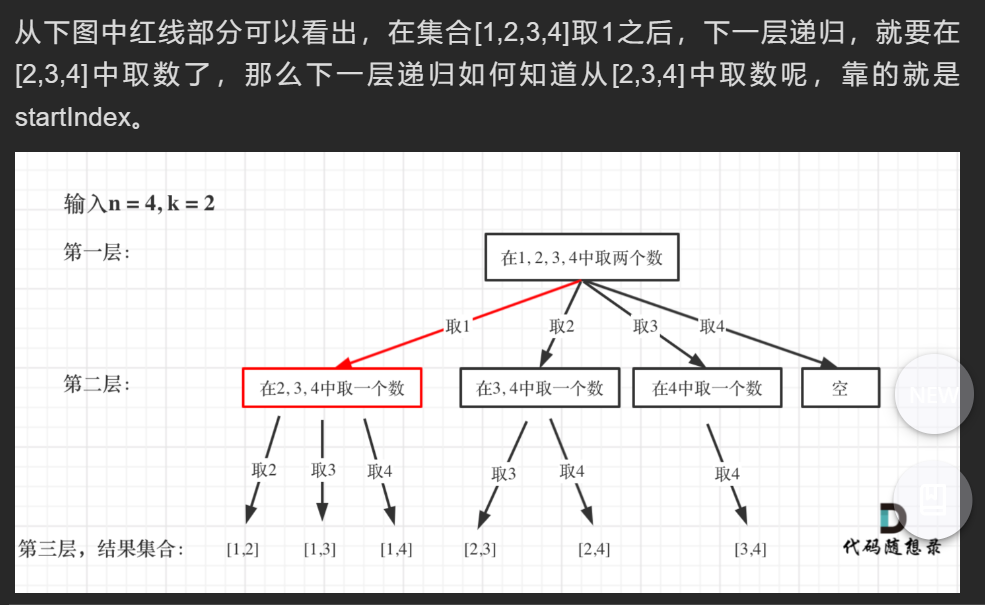
3.递归内部结构：

①temp这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合，用result把temp保存起来，并终止本层递归。

②for循环用来横向遍历树（集合元素），for循环每次从startIndex开始遍历，然后用path保存取到的节点i，再使用backtracking()进行递归下一层，最后再进行回溯的操作，撤销本次处理的结果。

剪枝优化：i <= n - (k - temp.size()) + 1

看上图当n = 4, k=3 时，起始位置最多只能取到2，才能满足后续有三个数字。取3，4后都不能满足我们需要的三位数取也没有意义了。

过程：

优化过程如下：

①已经选择的元素个数：temp.size();

②还需要的元素个数为: k - temp.size();

③在集合n中至多要从该起始位置 : n - (k - temp.size()) + 1，开始遍历

加1的意义：当n = 4, k=3 时，加入temp.size() = 0时，最多只能取到2，4 -（3-0）+1 =2，从1-2开始搜索都可以，超过2就不行了，不满足三个元素了。

代码：

 1 class Solution {
 2     List<List<Integer>> result = new ArrayList<>();
 3     List<Integer> temp = new ArrayList<>();
 4     public List<List<Integer>> combine(int n, int k) {
 5         int startIndex = 1;
 6         backatring(n, k, startIndex);
 7         return result;
 8     }
 9     public void backatring(int n, int k, int startIndex){
10         if (temp.size() == k){
11             result.add(new ArrayList<>(temp));
12             return;
13         }
14         for (int i = startIndex; i <= n - (k - temp.size()) + 1; i++){
15             temp.add(i);
16             backatring(n, k, i+1);
17             temp.remove(temp.size() - 1);
18         }
19     }
20 }