HDU-5738

Eureka

Time Limit: 8000/4000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Problem Description

Input

There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:
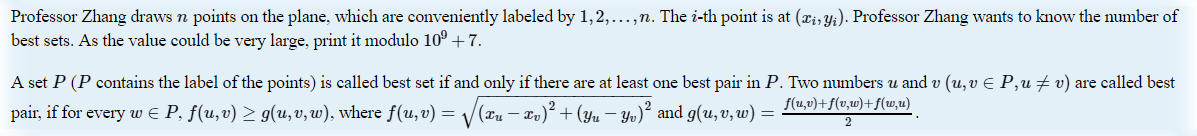
The first line contains an integer n (1≤n≤1000) -- then number of points.
Each of the following n lines contains two integers xi and yi (−109≤xi,yi≤109) -- coordinates of the i-th point.

 

Output

 For each test case, output an integer denoting the answer.

 

Sample Input

3

3

1 1

1 1

1 1

3

0 0

0 1

1 0

1

0 0

 

Sample Output

4

3

0　

 

Source

2016 Multi-University Training Contest 2

 

题解：给出n个整点，定义f(u,v)为u和v的距离，g(u,v,w)=((f(u,v)+f(u,w)+f(v,w))/2，定义这n个点的非空子集P是最好的当且仅当P中含有一个最好点对(u,v)，最好点对定义是，对集合P中任一点w，(u,v)满足f(u,v)>=g(u,v,w)，问有多少种不同的最好集合 .

 

思路：由f(u,v)>=g(u,v,w)知f(u,v)>=f(u,w)+f(v,w)，显然w需要在以u和v为端点的线段上，故问题转变为这n个点能构成多少种不同的线段（此处不同指的是两个端点的编号不同时相同，线段可以左右端点相同），首先去重，将所有重点去掉只留一个同时记录其数量，枚举线段左端点，将其他所有点与此点的横纵坐标差值(x,y)化成即约形式后存在map中，那么最后这个map中存的就是以该点为左端点，其他点为右端点构成线段的所有可能斜率以及每个斜率对应的点数，假设斜率为k的有res个点，该点重复次数是num，之后就可以开始计数，即求以该点为左端点，斜率为k的线段有多少个，即从num个重复的端点中任选不少于一个点，简单推导可得共有(2^num-1)*(2^res-1)种，从res个点中任选不少于一个点的方法数，这样枚举完左端点后就得到了所有左右端点不同的线段的数量，但还要把左右端点相同的线段加到答案中，这个只需要枚举每个重点，例如某个点重复了num次，那么其对答案的贡献就是从中选取不少于两个点的方法数，即2^num-num-1，上面的贡献全部累加起来即为答案.

(转载：http://blog.csdn.net/v5zsq/article/details/52045420)

 

代码：

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<map>
 using namespace std;
 typedef long long ll;
 #define maxn 1111
 #define mod 1000000007ll
 struct node
 {
     int x,y,num;
 }a[maxn];
 int T,n;
 typedef pair<int,int>P;
 map<P,int>m;
 map<P,int>::iterator it;
 ll f[maxn];
 int cmp(node a,node b)
 {
     if(a.x!=b.x)return a.x<b.x;
     if(a.y!=b.y)return a.y<b.y;
     return a.num>b.num;
 }
 int gcd(int a,int b)
 {
     return b?gcd(b,a%b):a;
 }
 int main()
 {
     f[]=;
     for(int i=;i<maxn;i++)f[i]=f[i-]*2ll%mod;
     scanf("%d",&T);
     while(T--)
     {

         scanf("%d",&n);
         for(int i=;i<n;i++)
             scanf("%d%d",&a[i].x,&a[i].y);
         sort(a,a+n,cmp);
         int cnt=;
         for(int i=;i<n;i++)
         {
             int num=;
             while(i<n-&&a[i].x==a[i+].x&&a[i].y==a[i+].y)num++,i++;
             a[cnt].x=a[i].x,a[cnt].y=a[i].y,a[cnt++].num=num;
         }
         sort(a,a+cnt,cmp);
         ll ans=;
         for(int i=;i<cnt;i++)
         {
             ll temp=(f[a[i].num]-a[i].num-)%mod;
             ans=(ans+temp+mod)%mod;
         }
         for(int i=;i<cnt;i++)
         {
             m.clear();
             for(int j=i+;j<cnt;j++)
             {
                 int x=a[j].x-a[i].x,y=a[j].y-a[i].y;
                 int g=gcd(abs(x),abs(y));
                 x/=g,y/=g;
                 P p=make_pair(x,y);
                 m[p]+=a[j].num;
             }
             for(it=m.begin();it!=m.end();it++)
             {
                 ll temp=(f[a[i].num]-)*(f[it->second]-)%mod;
                 ans=(ans+temp+mod)%mod;
             }
         }
         printf("%I64d\n",ans);
     }
     return ;
 }