深度学习的优化器（各类 optimizer 的原理、优缺点及数学推导）

深度学习优化器

深度学习中的优化器均采用了梯度下降的方式进行优化，所谓炼丹我觉得优化器可以当作灶，它控制着火量的大小、形式与时间等。

初级的优化器

首先我们来一下看最初级的灶台（100 - 1000 元）

Batch Gradient Descent (BGD)

名字叫做批梯度下降，实际上每次迭代会使用全部的数据来更新梯度（应该是取所有数据的平均梯度），具体公式如下：

\[\theta = \theta - \eta \cdot \nabla_{\theta} J(\theta)
\]

伪代码如下：

for i in range(epochs):
    grad = eval_grad(losses, dataset, params)
    params = params - lr * grad

由上可知，每一个 epoch 更新一次梯度，每更新一次梯度需要使用全部数据。那么我们基本可以总结：

• 优点：如果是凸优化一定能取得全局最优解，如果是非凸优化可以取得局部最优解。
• 缺点： 如果数据量过大会使得优化时间变长，优化变得十分缓慢，而且对 memory 也有一定要求。

Stochastic Gradient Descent (SGD)

随机梯度下降的公式如下：

\[\theta = \theta - \eta \cdot \nabla_{\theta}J(\theta;x^{(i)};y^{(i)})
\]

SGD 可以避免 BGD 因为大数据集而造成的冗余计算，比如 BGD 会对相似的数据进行重复计算。SGD 则是每次只选择一个样本的数据来进行更新梯度，伪代码如下：

for i in range(epochs):
    random_shuffle(dataset)
    for data_i in dataset:
	grad = eval_grad(losses, data_i, params)
	params = params - lr * grad

由上很容易知道，SGD 每次更新只用一个数据，因此其优化之路像一个喝醉酒的醉汉一样。这其实也是有利有弊的：

• 优点：
  • 由于一次只用一个数据，因此梯度更新很快
  • 当然也可以进行在线学习（不用收齐所有数据）
  • 也会处于一个高 variance 的状态，更新时 loss 比较震荡，可能会使得其跳出局部最优点到达一个更好的局部最优。
• 缺点：
  • 也正因为震荡，很难收敛于一个精准的极小值。
    
    但实验表明，只要对学习率进行调整就可以使得 SGD 的最终收敛效果与 BGD 一致。

Mini-Batch Gradient Descent

小批量随机梯度下降可以看作是 SGD 和 BGD 的中间选择，每次选择数量为 n 的数据进行计算，既节约的每次更新的计算时间和成本，也减少了 SGD 的震荡，使得收敛更加快速和稳定。其公式为：

\[\theta = \theta - \eta \cdot \nabla_{\theta}J(\theta;x^{(i:i+n)};y^{(i:i+n)})
\]

伪代码如下：

for i in range(epochs):
    random_shuffle(dataset)
    for batch_data in dataset:
	grad = eval_grad(losses, batch_data, params)
	params = params - lr * grad

这应该也是我们平时真正使用的随机梯度下降，当 n = 1 时，MiniBGD = SGD，n = len(dataset) 时 MiniBGD = BGD。

至此，初级灶台虽说有所改进，但是仍然存在一下问题：

• 选择合适的学习率仍然是一个玄学
• 学习率 schedule 需要预设不能自适应数据集的特点
• 学习率针对所有参数，而并非所有参数需要同样的学习率
• 对于非凸问题极易陷入局部最优

进阶的优化器

再来看一下进阶的灶台（1000 - 5000元）

Momentum

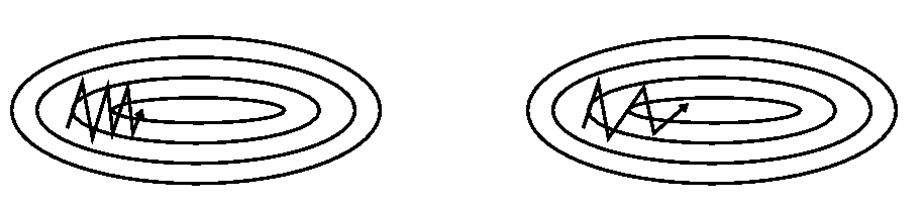
看到动量这个单词，我们不妨将优化想象为物理过程。如果将优化的空间比作现实的地形，地形的最低点是我们的目的地，优化的过程想象为需要将一辆小车到最低点，而优化器负责控制驱动（加减速、方向），数据的梯度则是负责操纵优化器的司机。

SGD 是每次选择一个数据进行梯度更新，在”峡谷“地带时，梯度经常异号就 loss 反复震荡（如上图）。这好比这辆车每开一步就换了一个司机（数据产生的梯度），每个司机的想法都不同。特别是到局部最优的时候，由于梯度始终为 0 使得每个司机上车后都说刹车别走。

而 Momentum 会使 SGD 虽然每一步都要换司机，但是这个司机必须参考之前开过车所有司机的意见，当然主要参考最近几次的，这样即便在局部最优，新司机觉得应该刹车（梯度为零）但是刚下车的几位司机都认为应该向前冲，这使得小车可能冲过局部最优（避免陷入局部最优），在峡谷地形也会因为会参考几个司机的建议（其实这里近似于一个 mini-batch）而过分震荡（如上图），公式如下：

\[\begin{aligned}
v_t &= \gamma v_{t-1} + \eta \nabla_{\theta} J(\theta_{t-1}) \\
\theta_t &= \theta_{t-1} - v_t
\end{aligned}
\]

这就好像模拟将小球放在上坡，松手后，滚下坡去，它并不会在最低点直接停住，它会冲上对坡（因为有惯性，有动量）。要么冲出去；要么折回来反复，最后因为能量耗尽停在最低点。

Nesterov Accelerated Gradient

Momentum 虽然会使考虑之前梯度与当前梯度来决定当前权重如何更新，但是它还不够聪明，它不会预测未来可能的情况。由上面最后一式我们可以知道权重是由动量项更新的 \(v_t\) 来进行更新。我们来看看 NAG 是如何做的：

\[\begin{aligned}
v_t &= \gamma v_{t-1} + \eta \nabla_{\theta} J(\theta_{t-1} - \gamma v_{t - 1}) \\
\theta_t &= \theta_{t-1} - v_t
\end{aligned}
\]

式中使用 \(\theta - \gamma v_{t - 1}\) 来近似预测未来的权重，并对它求导求得未来近似的梯度，来告诉权重未来可能的变化，并进行调整（以至于不在冲坡的时候过猛）。

智能的优化器

最后是智能的灶台（5000 - 10000 元），之前的灶台都要预先指定火的大小而且对所有食材用同样大小的火，那有没有更智能的灶台可以自己随着烹饪时间甚至自己根据食材来控制火候呢？答案是肯定有的（不然叫什么人工智能^_-)。不过在介绍这个之前，我们先来看一个指数加权平均和偏差修正两个技巧。

指数加权平均 & 偏差修正

公式推导如下：

\[\begin{aligned}
v_t &= \beta v_{t-1} + (1 - \beta)\theta_{t} \\
v_{t-1} &= \beta v_{t-2} + (1 - \beta)\theta_{t - 1} \\
&\dots \\
v_{1} &= \beta v_{0} + (1 - \beta)\theta_{1}
\end{aligned}
\]

将上列等式由下分别迭代至上一式，并得知初始条件 \(v_{0}=0\)。

\[v_t = (1 - \beta)\beta\theta_{t - 1} + (1 - \beta)\beta^2\theta_{t - 2} + \cdots + (1 - \beta)\beta^{n - 1}\theta_{1}
\]

\(\beta\) 一般是一个小于 1 的数，由上式可知 t 时刻的变量会由前 t - 1 个时刻的变量共同决定，但每个变量前加了一个关于 \(\beta\) 的指数级系数，离 t 时刻越远的权重越小，若是 \(\beta =0.9\) 第 20 个数的权重都在 0.01 左右了，后面的影响会更小。指数平均加权由此而来。其实我们很容易发现：

\[v_{1} = (1 - \beta)\theta_{1}
\]

由于最初始的变量没有多的变量可以平均，再加上 \((1 - \beta)\) 又很小，因此我们需要对初始时刻的变量进行一个修正：

\[\hat{v}_{t} = \frac{v_{t}}{1 - \beta^t}
\]

上式可以解决由于在初期没有变量可以平均的问题，使得 \({v}_{t} = \theta_{t}\)。

Adagrad

Adagrad 是一种自适应梯度的优化器，它有什么特点呢？它对不同参数使用不同的学习率，对于更新频率较低的参数施以较大的学习率，对于更新频率较高的参数用以较小的学习率。我们先来看一下公式：

\[g_{t,i} = \nabla_{\theta_t}J(\theta_{t, i})
\]

\(g_{t,i}\) 代表了第 t 步的第 i 个参数 \(\theta_{t, i}\) 的梯度，梯度更新则使用下列式子：

\[\theta_{t + 1, i} = \theta_{t, i} - \frac{\eta}{\sqrt{G_{t,ii}+\epsilon}} \cdot g_{t,i} \tag{a*}
\]

\(G_t \in \mathbb{R}^{d \times d}\) 是一个对角矩阵，对角线上的元素 \(G_{t,ii}\) 计算如下：

\[G_{t,ii} = G_{t - 1,ii} + g_{t, i}^2 = \sum_{k = 0}^t g_{k, i}^2
\]

其实很容易发现，它就是 t 步之前所有步数关于参数 \(\theta_i\) 的平方和。可以看得出，如果 \(\theta_i\) 频繁更新，那么梯度肯定不为零，其平方必然大于零，(a*) 式中的 \(G_{t,ii}\) 会随着更新次数的积累变得越来越大，分母越大，学习率变小，从而调小了 \(\theta_i\) 的学习率，比较而言更新少的学习率就大一些了。其总体的公式为：

\[\theta_{t} = \theta_{t - 1} - \frac{\eta}{\sqrt{G_{t - 1}+\epsilon}} \odot g_{t - 1}
\]

实际上，Adagrad 在优化稀疏数据的时候表现会比较好，但是其缺点也是显而易见的，由于 \(G_{t,ii}\) 是一个非负数，随着步数增加很容易越累积越大，从导致学习率过早变小，学习缓慢。

Adadelta & RMSprop

对于这个问题 Adadelta & RMSprop 几乎是在同一时间提出了改进方案。这里只介绍 Adadelta 改进的最终版本，首先对梯度平方的累积改为了：

\[E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma)g^2_t
\]

上式其实就是使用了指数加权平均，使得第 t 步的 \(E[g^2]_t\) 只累加了离 t 较近的步数的梯度平方。每步权重更新的步长如下（并用均方根 RMS 进行表示）：

\[\Delta \theta_t = -\frac{\eta}{\sqrt{E[g^2]_t + \epsilon}}g_t = -\frac{\eta}{RMS[g]_t}g_t
\]

同时使用了指数加权平均来计算了步长的均方根：

\[\begin{aligned}
E[\Delta\theta^2]_t &= \gamma E[\Delta\theta^2]_{t-1} + (1 - \gamma)\Delta\theta^2_t \\
RMS[\Delta\theta]_t &= \sqrt{E[\Delta\theta^2]_t + \epsilon}
\end{aligned}
\]

可能会比较疑惑计算这个干嘛呢？这里我们先讲一下牛顿法，其公式如下：

\[x_n = x_{n-1} - \frac{f^{\prime}(x_{n-1})}{f^{\prime \prime}(x_{n-1})}
\]

可以看出来其将二阶导数的倒数作为”学习率“，所以一阶导数和二阶导数之比为步长即 \(\Delta x\)，即有下列推导：

\[\begin{aligned}
\because \quad&\Delta \theta \approx \frac{J^{\prime}(\theta)}{J^{\prime \prime}(\theta)} \\
\therefore \quad&\frac{1}{J^{\prime \prime}(\theta)} = \frac{\Delta \theta_t}{J^{\prime}(\theta)} \approx -\frac{RMS[\Delta\theta]_{t-1}}{RMS[g]_{t}}
\end{aligned}
\]

首先解释一下，这里没有用 \(RMS[\Delta\theta]_{t}\) 是因为 \(\Delta \theta_t\) 还没算出来。这里基本可以理解为使用了 \(\Delta \theta_t\) 的均方根来近似 \(\Delta \theta_t\) 的值，使用了 \(g_t\) 的均方根来近似一阶导数的值，从而近似了二阶导数的倒数，最后 Adadelta 权重更新式子为：

\[\theta_t = \theta_{t-1} - \frac{RMS[\Delta\theta]_{t-2}}{RMS[g]_{t-1}}g_{t-1}
\]

可见，Adadelta 甚至不需要指定学习率，RMSprop 思想大致相同，其更新公式如下：

\[\theta_t = \theta_{t-1} - \frac{\eta}{RMS[g]_{t-1}}g_{t-1}
\]

Adam

Adaptive Moment Estimation 有点像是 Momentum 和 RMSProp 的结合体，首先对梯度，梯度的平方使用指数加权平均：

\[\begin{aligned}
m_t = \beta_1 m_{t-1} + (1 - \beta_1)g_t \\
v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2
\end{aligned}
\]

然后对其进行偏差修正：

\[\begin{aligned}
\hat{m}_t = \frac{m_{t}}{1 - \beta_1^t} \\
\hat{v}_t = \frac{v_{t}}{1 - \beta_2^t}
\end{aligned}
\]

最后权重的更新公式如下：

\[\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\hat{v}_{t-1}}+\epsilon}\hat{m}_{t-1}
\]

原理就不过多介绍了，一般设置 \(\beta_1 = 0.9, \beta_2=0.999\)，Adam 被认为是泛化极好，比起其他优化器性能也更好，并且是训练神经网络的首选。

AdamW

AdamW 想做的最主要是认为在使用 L2 正则化时，Adam 没有正确使用。当我们使用 L2 正则化时，会在 loss 后面添加一个权重的平方项。比如我们如果使用的 SGD 则权重更新的表达式为（最后一项是正则化项）：
$$
\theta_t = \theta_{t-1} - \eta \cdot \nabla J(\theta_{t-1}) - \eta \lambda \theta_{t-1}
$$
如上图所示，当我们使用动量的时候，实际上这里的正则化不再与 SGD 中的相同，因为动量会累积之前的梯度，因此当使用动量的时候，权重更新的公式为：
$$
\theta_t = \theta_{t-1} - m_t - (1 - \beta)\beta \eta\lambda\theta_{t - 1} + (1 - \beta)\beta^2\eta\lambda\theta_{t - 2} + \cdots
$$
聪明的小朋友已经发现了！因为动量里面还有过往的梯度，因此在使用正则化的时候不能进行解耦，实际上的正则化项会包含以前的正则化项，当然像 Adam 还有一个梯度平方的累积就更不纯粹了。于是 AdamW 直接在进行更改实现与无动量的 SGD 一样的正则化：
$$
\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\hat{v}_{t-1}}+\epsilon}\hat{m}_{t-1} - \eta \lambda \theta_{t-1}
$$
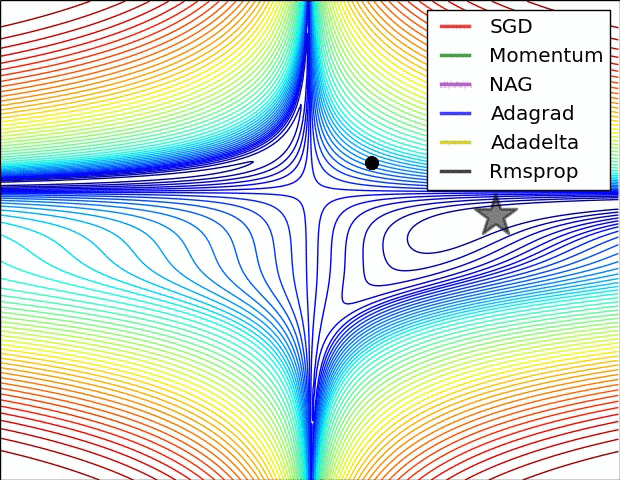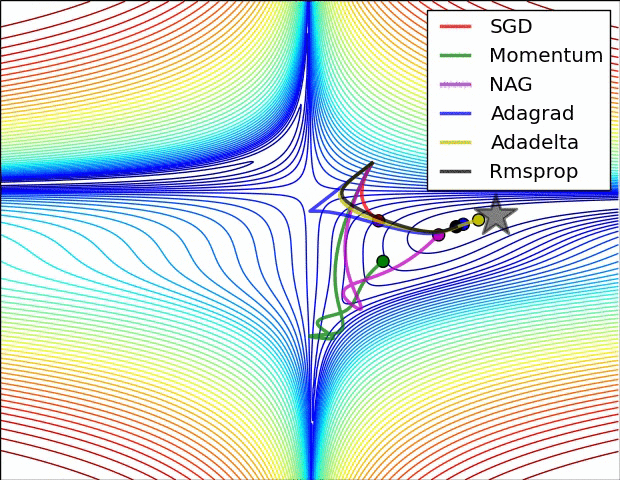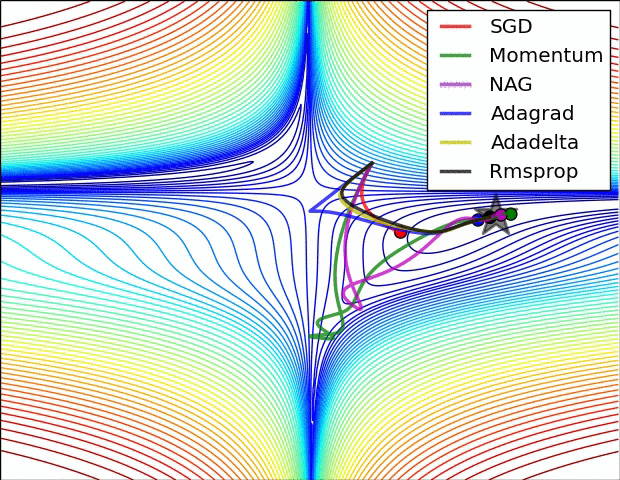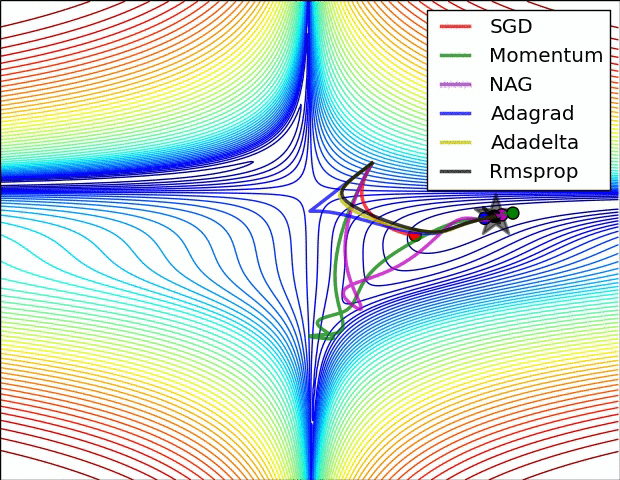
最后我们来看看几种优化器的效果图吧！