AcWing1264. 动态求连续区间和 (树状数组做法)

1、题目

给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。

输入格式

第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。

第二行包含 n 个整数，表示完整数列。

接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。

数列从 1 开始计数。

输出格式

输出若干行数字，表示 k=0 时，对应的子数列 [a,b] 的连续和。

数据范围

\[1≤n≤100000,
1≤m≤100000，
1≤a≤b≤n
\]

输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

输出样例：

11
30
35

2、题意分析

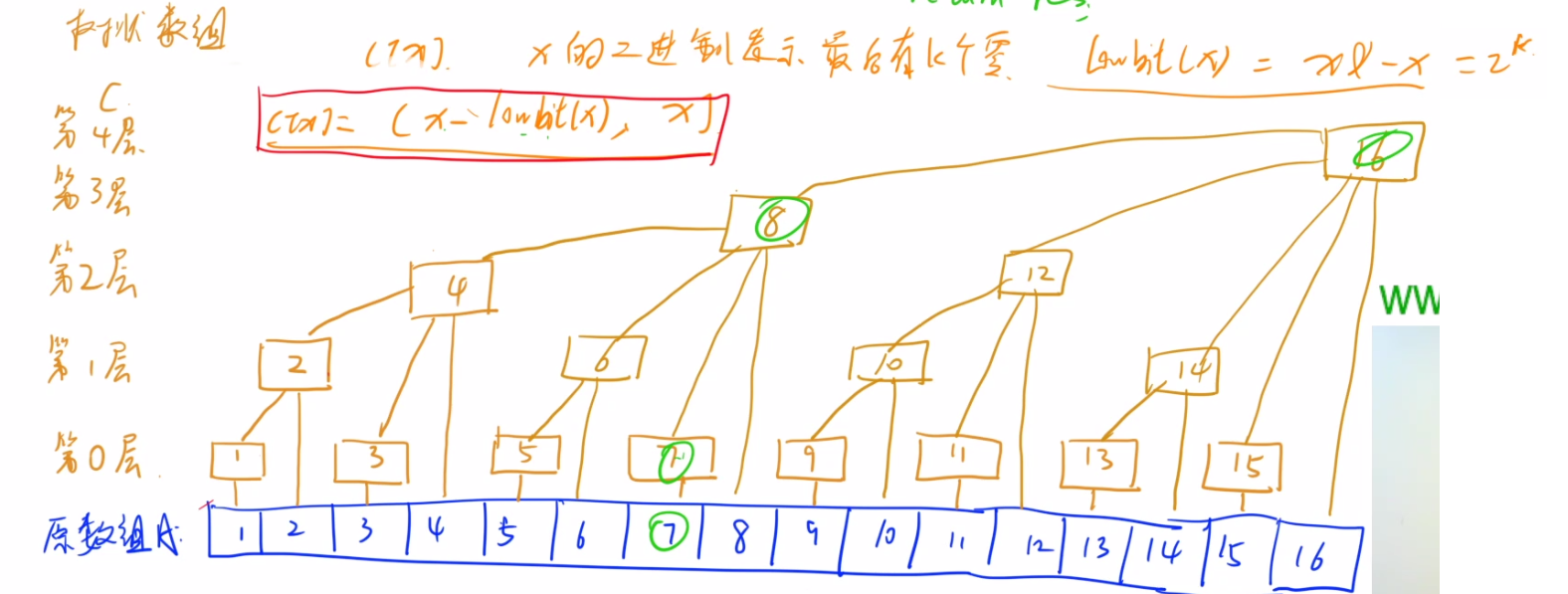
1、知识点

本题考查树状数组的使用、树状数组用起来的时间复杂度为O(logn)、操作一共有以下两种：

1、给某个位置上的数加上一个数

void add(int x, int v)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

2、求某一个前缀和

int query(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

3、附加lowbit操作

int lowbit(int x)
{
    return x & -x;
}

2、具体分析（略）

---

3、代码

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 100010;

int a[N], tr[N];
int n, m;

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int v)
{
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

int query(int x)
{
    int res = 0;
    for(int i = x; i ; i -= lowbit(i)) res += tr[i];
    return res;
}
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n ; i ++) scanf("%d", &a[i]);
    for(int i = 1; i <= n ; i ++) add(i, a[i]);

    while(m --)
    {
        int k, x, y;
        scanf("%d%d%d", &k, &x, &y);
        if(k == 0) printf("%d\n", query(y) - query(x - 1));
        else add(x, y);
    }
    return 0;
}