基于主成分分析（PCA）的数据降维

一、概述

主成分分析（Principal Component Analysis，PCA）是一种用于数据降维的方法，其核心目标是在尽可能保留原始数据信息的前提下，将高维数据映射到低维空间。该算法基于方差最大化理论，通过寻找数据的主要变化方向（即主成分），将原始数据投影到这些方向上，从而实现降维。

二、算法过程

1.数据中心化

指将数据的每个特征减去其均值，使得数据的均值为 0。这样做的目的是将数据的分布中心移到原点，便于后续计算协方差矩阵等操作，因为协方差矩阵的计算对于数据的中心位置比较敏感，中心化后可以更好地反映数据的内在结构和相关性。

值得说明的是，在某些情况下，特别是当不同特征的量纲差异较大或者数据的分布比较复杂时，除了数据中心化外，还会进行数据标准化。数据标准化是指将数据的每个特征减去对应特征列的均值再除以标准差，这样可以进一步消除不同特征在尺度上的差异，使得不同特征在后续的分析中具有相同的重要性，避免因特征尺度不同而导致的结果偏差。

2. 计算协方差矩阵

对中心化后的数据矩阵计算协方差，协方差矩阵描述了数据特征之间的相关性。

总体协方差矩阵计算公式为 $Cov=\frac{1}{n}X_{c}^{T}X_c$

样本协方差矩阵计算公式为 $S=\frac{1}{n-1}X_{c}^{T}X_{c}$

其中$n$是样本数量。实际计算中通常使用样本协方差，其中的$\frac{1}{n-1}$是总体协方差的无偏估计。

3. 计算协方差矩阵的特征值和特征向量

通过求解协方差矩阵$S$的特征方程 $\left| S-\lambda I \right|=0$ ，得到特征值$\lambda_i$和对应的特征向量$v_i$。特征值反映了数据在对应特征向量方向上的方差大小，特征值越大，说明数据在该方向上的变化程度越大，包含的信息越多。

4. 选择主成分

将特征值按照从大到小的顺序排列，对应的特征向量也随之重新排序。选择前 $k$ 个最大的特征值及其对应的特征向量，这些特征向量构成了新的低维空间的基向量。$k$ 的选择通常基于一个阈值，例如保留能够解释原始数据方差累计百分比达到一定比例（如 80%、90% 等）的主成分。

5.数据投影

将原始数据投影到由选定的 $k$ 个特征向量构成的低维空间中，得到降维后的数据。投影的计算公式为

\[Y=X_cW
\]

其中，$X_c$是中心化后的数据矩阵，$W$是由前$k$个特征向量组成的投影矩阵，$Y$ 是降维后的数据矩阵。

三、示例

现有一组二维数据 $X=
\begin{bmatrix}
1 & 2 \\
2 & 3 \\
3 & 4 \\
4 & 5 \\
5 & 6
\end{bmatrix}$ ，下面使用PCA方法进行降维，将其从二维降至一维。

1.数据标准化

首先，计算每列的均值：

第一列均值：$\bar x_1=\frac{1+2+3+4+5}{5}=3$

第二列均值：$\bar x_2=\frac{2+3+4+5+6}{5}=4$

然后，对矩阵$X$进行中心化，得到矩阵$X_c$

$X_c=$$\begin{bmatrix}
1-3 & 2-4 \\
2-3 & 3-4 \\
3-3 & 4-4 \\
4-3 & 5-4 \\
5-3 & 6-4
\end{bmatrix}$$=$$\begin{bmatrix}
-2 & -2 \\
-1 & -1 \\
0 & 0 \\
1 & 1 \\
2 & 2
\end{bmatrix}$

2. 计算协方差矩阵

协方差矩阵$S$的计算公式为$S=\frac{1}{n-1}X_{c}^{T}X_{c}$，其中$n$是样本数量。

$X_c^TX_c=$$\begin{bmatrix}
-2 & -1 &0 & 1 & 2 \\
-2 & -1 &0 & 1 & 2
\end{bmatrix}$$\begin{bmatrix}
-2 & -2 \\
-1 & -1 \\
0 & 0 \\
1 & 1 \\
2 & 2
\end{bmatrix}$$=$$\begin{bmatrix}
10 & 10 \\
10 & 10
\end{bmatrix}$

则协方差矩阵 $S$ 为

$S=\frac{1}{5-1}$$\begin{bmatrix}
10 & 10 \\
10 & 10
\end{bmatrix}$$=$$\begin{bmatrix}
2.5 & 2.5 \\
2.5 & 2.5
\end{bmatrix}$

3. 计算协方差矩阵的特征值和特征向量

对于矩阵 $S$，其特征方程为 $\left| S-\lambda I \right|=0$ ，其中 $I$ 是单位矩阵。

$\begin{vmatrix}
2.5-\lambda & 2.5 \\
2.5 & 2.5-\lambda
\end{vmatrix}$$=$${(2.5-\lambda)}^{2}-2.5^2$$=$$0$

展开可得 $\lambda^2-5\lambda=0$ ，解得特征值为 $\lambda_1=5$，$\lambda_2=0$。

求特征向量：

对于 $\lambda_1=5$ 求解 $(S-5I)v_1=0$

$\begin{bmatrix}
2.5-5 & 2.5 \\
2.5 & 2.5-5
\end{bmatrix}$$\begin{bmatrix}
v_{11} \\
v_{12}
\end{bmatrix}$$=$$\begin{bmatrix}
-2.5 & 2.5 \\
2.5 & -2.5
\end{bmatrix}$$\begin{bmatrix}
v_{11} \\
v_{12}
\end{bmatrix}$$=$$\begin{bmatrix}
0 \\
0
\end{bmatrix}$

取 $v_{11}=1$ ，则 $v_{12}=1$ ，单位化后得到特征向量 $v_1=
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}}
\end{bmatrix}$ 。

对于 $\lambda_2=0$ ，求解 $(S-0I)v_2=0$

$\begin{bmatrix}
2.5 & 2.5 \\
2.5 & 2.5
\end{bmatrix}$$\begin{bmatrix}
v_{21} \\
v_{22}
\end{bmatrix}$$=$$\begin{bmatrix}
0 \\
0
\end{bmatrix}$

取 $v_{21}=1$ ，则 $v_{22}=-1$ ，单位化后得到特征向量 $v_2=
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}}
\end{bmatrix}$ 。

4. 选择主成分

按照特征值从大到小排序，选择前 $k$ 个特征值对应的特征向量作为主成分。这里我们选择最大特征值 $\lambda_1=5$

对应的特征向量 $v_1=
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}}
\end{bmatrix}$ 作为主成分。

5. 数据投影

将中心化后的数据 $X_c$ 投影到主成分上，得到降维后的数据

$Y=X_cv_1=$$\begin{bmatrix}
-2 & -2 \\
-1 & -1 \\
0 & 0 \\
1 & 1 \\
2 & 2
\end{bmatrix}$$\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}}
\end{bmatrix}$$=$$\begin{bmatrix}
-2\sqrt{2} \\
-\sqrt{2} \\
0 \\
\sqrt{2} \\
2\sqrt{2}
\end{bmatrix}$ 。

四、Python实现

scikit-learn实现：

import numpy as np

from sklearn.decomposition import PCA

# 数据

data = np.array([[1, 2],

                 [2, 3],

                 [3, 4],

                 [4, 5],

                 [5, 6]])

# 创建PCA对象，指定降维后的维度为1

pca = PCA(n_components=1)

# 使用PCA对数据进行降维

reduced_data = pca.fit_transform(data)

# 降维后的数据

print("降维后的数据：")

print(reduced_data)

#### 函数实现：

import numpy as np

def pca(X, n_components):

    # 数据中心化

    X_mean = np.mean(X, axis=0)

    X_centered = X - X_mean

    # 计算协方差矩阵

    cov_matrix = np.cov(X_centered, rowvar=False)

    # 计算协方差矩阵的特征值和特征向量

    eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

    # 对特征值进行排序，获取排序后的索引

    sorted_indices = np.argsort(eigenvalues)[::-1]

    # 选择前n_components个最大特征值对应的特征向量

    top_eigenvectors = eigenvectors[:, sorted_indices[:n_components]]

    # 将数据投影到选定的特征向量上

    X_reduced = np.dot(X_centered, top_eigenvectors)

    return X_reduced

# 数据

X = np.array([[1,2],

              [2,3],

              [3,4],

              [4,5],

              [5,6]])

# 降至1维

n_components = 1

X_reduced = pca(X, n_components)

# 降维后的数据

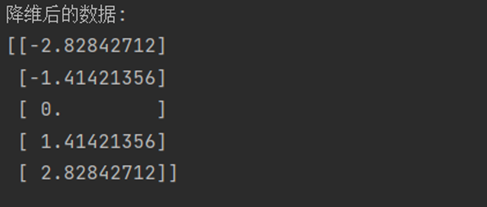
print("降维后的数据:")

print(X_reduced)

End.

下载