Bagging、Boosting、Stacking的原理

  Bagging、Boosting、Stacking是常见集成学习的形式，它们都是通过对多个学习器进行有机组合，达到比单个学习器性能更好的目标。

一、Bagging

1.算法概述

  Bagging（Bootstrap Aggregating）算法即自助聚合算法，是一种基于统计学习理论的集成学习算法，主要用于提高机器学习模型的稳定性和泛化能力。具体来说就是，先以Bootstrap方式（有放回重复采样）构造多个样本集，每个样本集分别训练得到一个学习器，最后将各学习器的输出综合起来，得到一个最终的输出，如果是分类，多采用多数投票的方式，如果是回归，采用取平均的方式，代表性算法如随机森林。

示意图

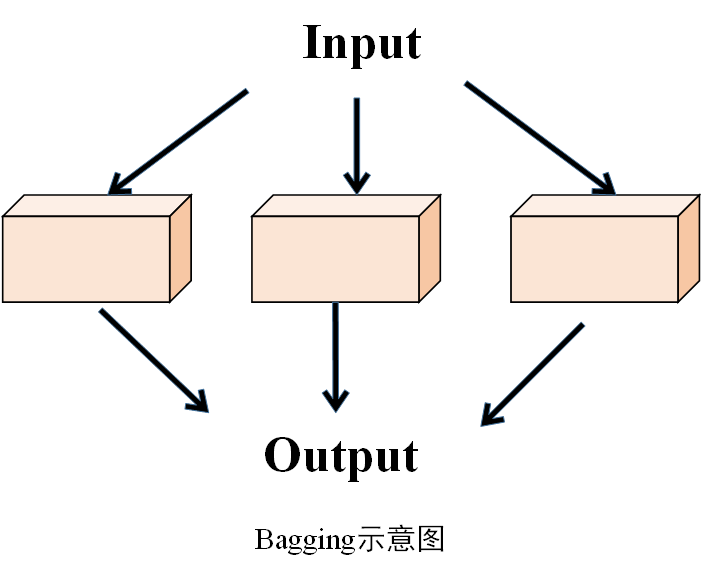
2.算法过程

(1) 数据采样

  从原始训练数据集\(D\)中，采用有放回的抽样方式，随机抽取 \(n\)个样本，组成一个新的训练数据集 \(D_i\)。这个过程会重复\(K\)次，从而得到\(K\)个不同的自助样本集\(\left\{ D_1,D_2,...,D_K \right\}\) 。由于是有放回抽样，每个自助样本集中可能会包含一些重复的样本，同时也会有一些原始数据集中的样本未被选中。

(2）模型训练

  对于每个自助样本集\(D_i\)，分别使用相同的基学习算法（如决策树、神经网络等）进行训练，得到\(K\)个不同的基模型\(\left\{ h_1,h_2,...,h_K \right\}\)。这些基模型在训练过程中会学习到不同的特征和模式，因为它们所使用的训练数据是不同的。

(3) 模型融合

  将训练好的\(K\)个基模型进行融合，以得到最终的预测结果。对于分类任务，通常采用投票法，即让\(K\)个基模型对测试样本进行预测，然后统计每个类别出现的次数，将得票最多的类别作为最终的预测结果。对于回归任务，一般采用平均法，即计算\(K\)个基模型对测试样本的预测值的平均值，将其作为最终的预测结果。

过程图示如下

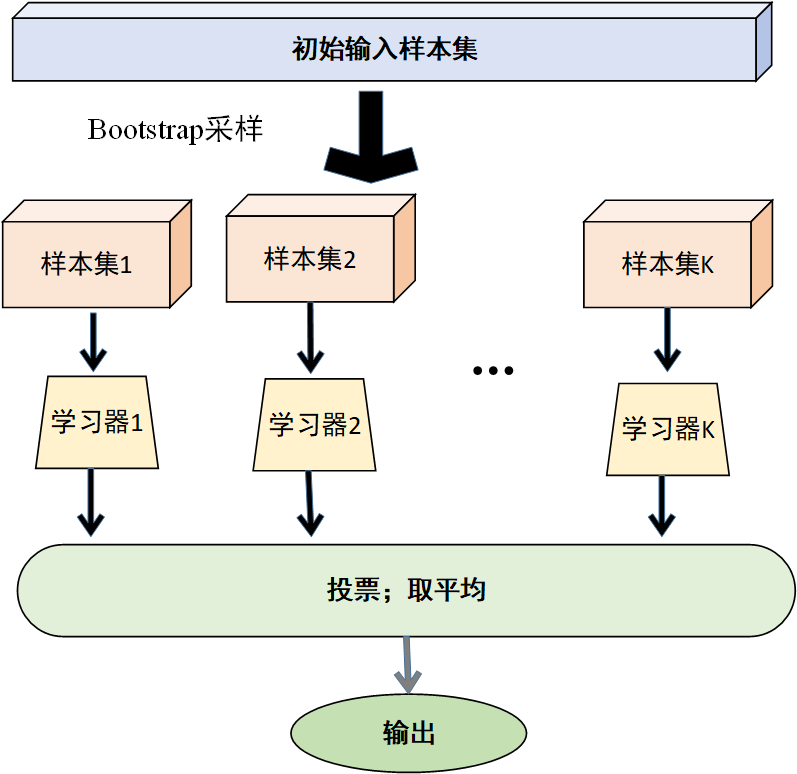
  通过 Bagging 算法，可以将多个基模型进行集成，充分利用它们之间的差异，降低模型的方差，从而提高模型的稳定性和泛化能力。尤其是在处理高方差的基模型（如决策树）时，Bagging 算法通常能取得较好的效果。

二、Boosting

1.算法概述

  Boosting是指逐层提升，其核心思想是“前人栽树，后人乘凉”，也就是使后一个学习器在前一个学习器的基础上进行增强，进而将多个弱学习器通过某种策略集成一个强学习器，以实现更好的预测效果。常见的提升算法如AdaBoost、XGBoost、CatBoost、LightGBM等。

示意图

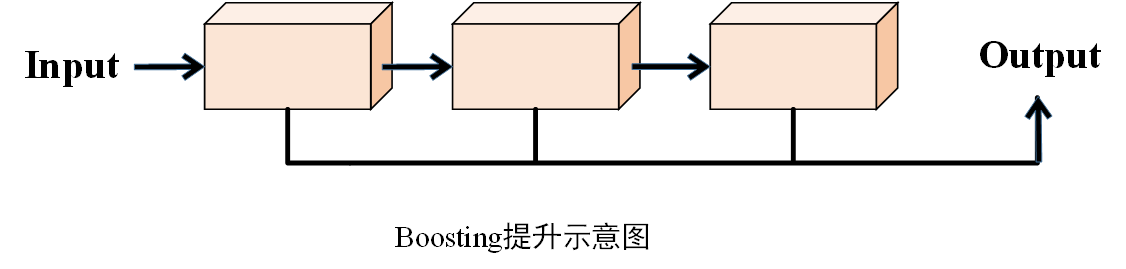
2.算法过程

（1）设置初始样本权重

  在算法开始时，为训练数据集中的每一个样本设定一个相同的权重。如对于样本集\(D=\left\{ (x_1,y_1),(x_2,y_2),...,(x_n,y_n) \right\}\)，初始权重为\(w^{(1)}=\left( w_{1}^{(1)} ,w_{2}^{(1)},...,w_{n}^{(1)} \right)\) ，其中\(w_{i}^{(1)}=\frac{1}{n}\)，即在第一轮训练时，每个样本在模型训练中的重要度是相同的。

（2）训练弱学习器​

  基于当前的权重分布，训练一个弱学习器。基于当前的权重分布，训练一个弱学习器。弱学习器是指一个性能仅略优于随机猜测的学习算法，例如决策树桩（一种简单的决策树，通常只有一层）。在训练过程中，弱学习器会根据样本的权重来调整学习的重点，更关注那些权重较高的样本。

(3) 计算弱学习器的权重

  根据弱学习器在训练集上的分类错误率，计算该弱学习器的权重。错误率越低，说明该弱学习器的性能越好，其权重也就越大；反之，错误率越高的弱学习器权重越小。通常使用的计算公式为

\[\alpha=\frac{1}{2}ln\left( \frac{1-\varepsilon}{\varepsilon} \right)
\]

  其中\(\varepsilon\)是该弱学习器的错误率。

(4) 更新训练数据的权重分布

  根据当前数据的权重和弱学习器的权重，更新训练数据的权重分布。具体的更新规则是，对于被正确分类的样本，降低其权重；对于被错误分类的样本，提高其权重。这样，在下一轮训练中，弱学习器会更加关注那些之前被错误分类的样本，从而有针对性地进行学习。公式为

\[\begin{equation} w_{i}^{(t+1)}=\frac{w_{i}^{(t)}}{Z_t}\cdot \begin{cases} e^{-\alpha_t}, \hspace{0.5em} if \hspace{0.5em} h_t(x_i)=y_i \\ e^{\alpha_t}, \hspace{0.5em} if \hspace{0.5em} h_t(x_i)\ne y_i \end{cases} \end{equation}
\]

  其中，\(w_{i}^{(t)}\)是第\(t\) 轮中第\(i\)个样本的权重，\(Z_t\)是归一化因子，确保更新后的样本权重之和为 1，\(h_t(x_i)\)是第\(t\)个弱学习器对第\(i\)个样本的预测结果。

(5) 重复以上步骤

  不断重复训练弱学习器、计算弱学习器权重、更新数据权重分布的过程，直到达到预设的停止条件，如训练的弱学习器数量达到指定的上限，或者集成模型在验证集上的性能不再提升等。

（6）构建集成模型

  将训练好的所有弱学习器按照其权重进行组合，得到最终的集成模型。如训练得到一系列弱学习器\(h_1,h_2,...,h_T\)及其对应的权重\(\alpha_1,\alpha_2,...,\alpha_T\)，最终的强学习器\(H(X)\)通过对这些弱学习器进行加权组合得到。对于分类问题，通常采用符号函数\(H\left( X \right)=sign\left( \sum_{t=1}^{T}{\alpha_th_t(X)} \right)\)输出；对于回归问题，则可采用加权平均的方式输出。

过程图示如下



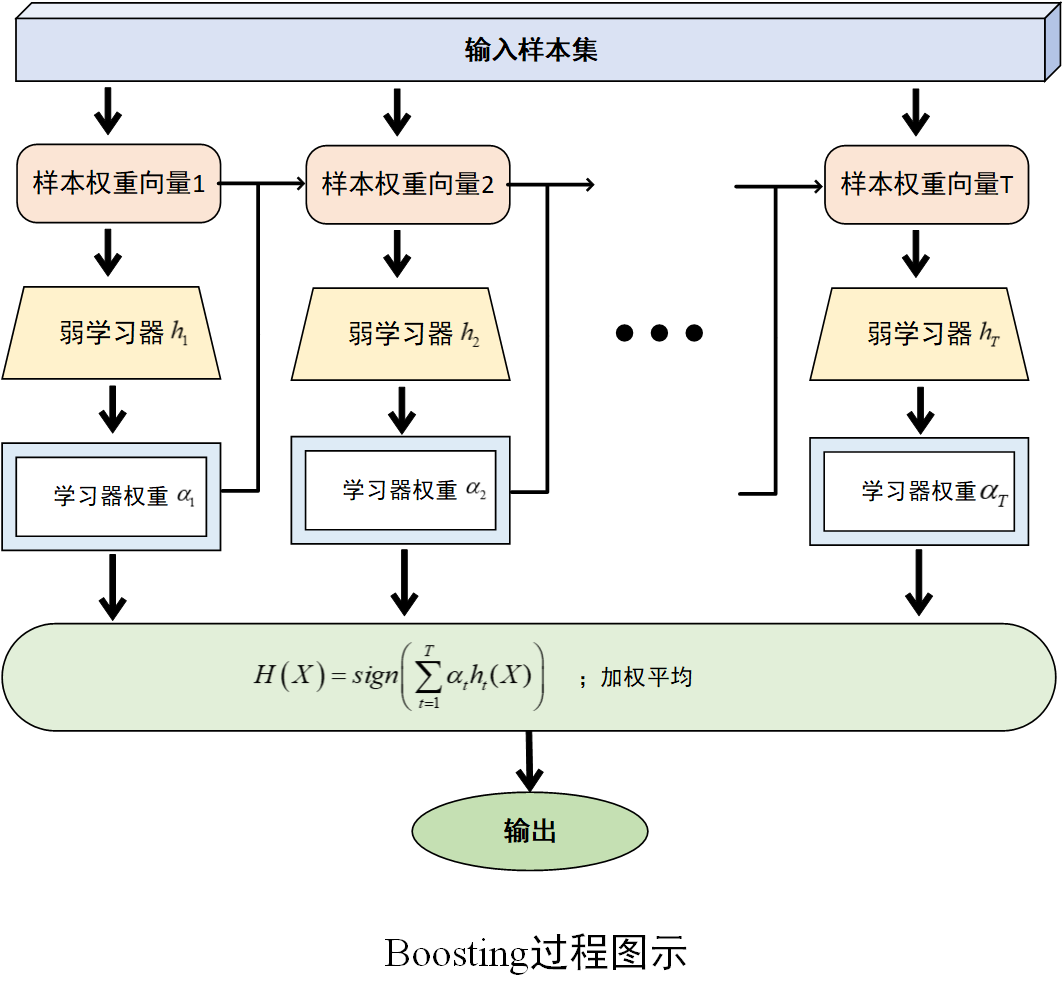
  通过以上过程，Boosting 算法能够不断调整样本权重，让后续的弱学习器更加关注之前被错误分类的样本，从而逐步提升模型的性能，将多个弱学习器集成起来形成一个性能较强的学习器。

三、Stacking

1.算法概述

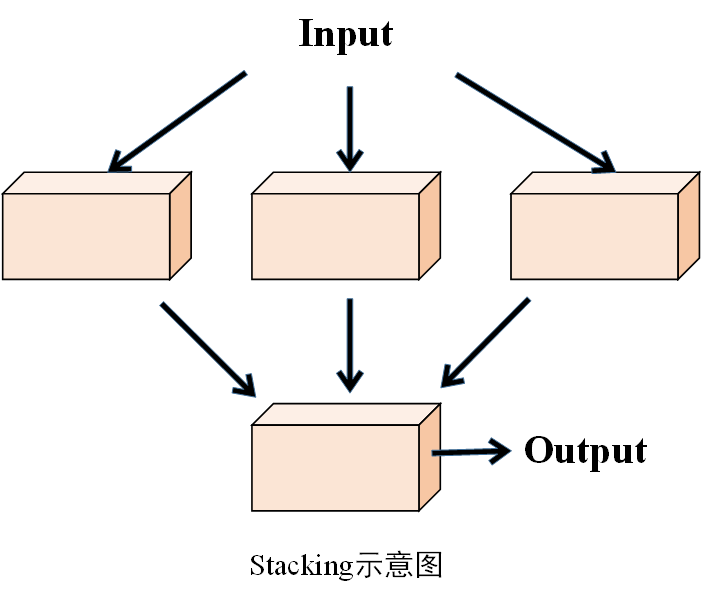
  Stacking（堆叠集成）算法也是一种集成学习方法，它通过组合多个基学习器的预测结果，训练一个更高层次的模型（元学习器），从而获得比单个模型更好的预测性能。其核心思想在于利用不同算法在处理数据时的互补性，通过多层学习，挖掘数据的特征和规律，以实现更准确的预测。

示意图

2.算法过程

(1)训练多个基学习器

  选择若干个不同的学习算法（如决策树、支持向量机、神经网络等）训练多个基学习器，记为\(h_1,h_2,...,h_K\)。

(2)构建新训练集

  将各基学习器在训练集上的预测值作为一个新的特征矩阵，与原始训练集的标签相组合，构成一个新的训练集。

(3)训练元学习器

  选择一个学习算法（如逻辑回归、决策树等）在新训练集上训练学习器，即元学习器。表达式为$$H\left( X \right)=F\left( h_1(X),h_2(X),...,h_K(X) \right)$$

过程图示如下



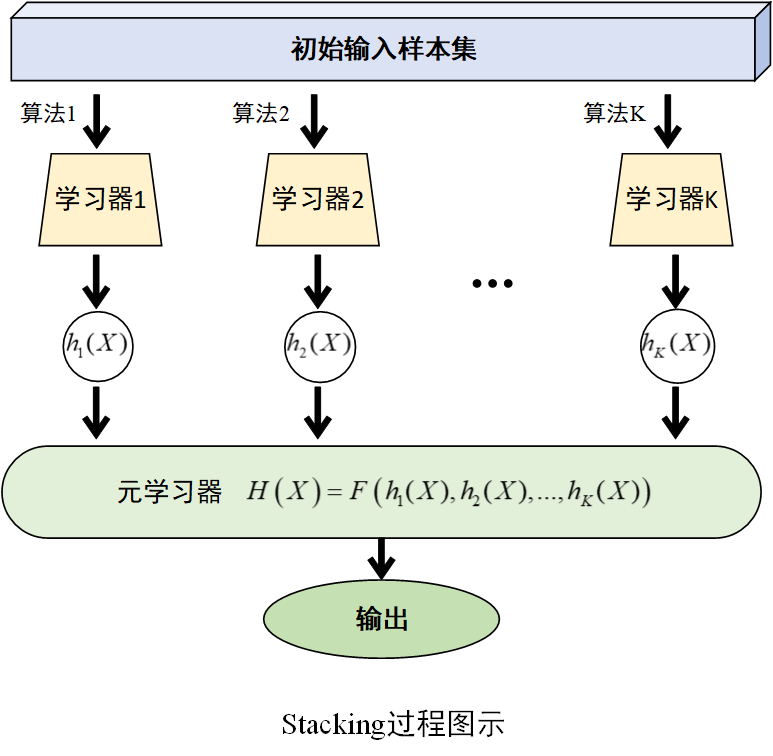
  Stacking方法将基学习器对数据的预测结果作为元学习器的输入特征，元学习器输出最终的预测结果。这种分层训练和预测的方式，能够充分利用不同算法的优势，捕捉数据中更复杂的关系。

End.

全文pdf下载