论文解读（SR-GNN）《Shift-Robust GNNs: Overcoming the Limitations of Localized Graph Training Data》

论文信息

论文标题：Shift-Robust GNNs: Overcoming the Limitations of Localized Graph Training Data
论文作者：Qi Zhu, Natalia Ponomareva, Jiawei Han, Bryan Perozzi
论文来源：2021, NeurIPS
论文地址：download 
论文代码：download

1 Introduction

　　半监督学习通过使用数据之间的关系（即边连接关系，会产生归纳偏差），以及一组带标签的样本，来预测其余部分的标签。

　　半监督学习存在的问题：训练数据集和测试数据集的数据分布不一致，容易产生 过拟合、泛化性差的问题。当数据集太小或太大，选择一部分带标记的子集进行训练，这类问题就显得比较明显。

　　具体来说，我们的贡献如下：

　　1. We provide the first focused discussion on the distributional shift problem in GNNs.
　　2. We propose generalized framework, Shift-Robust GNN (SR-GNN), which can address shift in both shallow and deep GNNs.
　　3. We create an experimental framework which allows for creating biased train/test sets for graph learning datasets.
　　4. We run extensive experiments and analyze the results, proving that our methods can mitigate distributional shift.

2 Related Work

　　标准学习理论假设训练和推理数据来自相同的分布，但在许多实际情况下，这不成立。在迁移学习中，领域自适应（Domain adaptation）问题涉及将知识从源域（用于学习）转移到目标域（最终的推理分布）。

　　[3] 作为该领域的开创性工作定义了一个基于模型在 源域 和 目标域 表现的距离度量函数来量化两域的相似性。为获得最终的模型，一个直观的想法是基于源数据和目标数据的加权组合来训练模型，其中权重是域距离的量化函数。

3 Distributional shift in GNNs

　　SSL 分类器，通常使用交叉熵损失函数 $l$：

　　　　$\mathcal{L}=\frac{1}{M} \sum\limits_{i=1}^{M} l\left(y_{i}, z_{i}\right)$

　　当训练数据和测试数据来自同一域  $\operatorname{Pr}_{\text {train }}(X, Y)=\operatorname{Pr}_{\text {test }}(X, Y)$  时，训练得到的分类器表现良好。

3.1 Data shift as representation shift

　　基于标准学习理论的基础假设 $\operatorname{Pr}_{\text {train }}(Y \mid Z)=\operatorname{Pr}_{\text {test }}(Y \mid Z)$，分布位移的主要原因是表示位移，即 　　　

　　　　$\operatorname{Pr}_{\text {train }}(Z, Y) \neq \operatorname{Pr}_{\text {test }}(Z, Y) \rightarrow \operatorname{Pr}_{\text {train }}(Z) \neq \operatorname{Pr}_{\text {test }}(Z)$

　　本文关注的是训练数据集和测试数据集表示 $Z$ 之间的分布转移。

　　为衡量这种变化，可使用 MMD[8] 或 CMD[37] 等差异指标。CMD 测量分布 $\mathrm{p}$ 和 $\mathrm{q}$ 之间的直接距离，如下：

　　　　$\mathrm{CMD}=\frac{1}{|b-a|}\|\mathrm{E}(p)-\mathrm{E}(q)\|_{2}+\sum\limits _{k=2}^{\infty} \frac{1}{|b-a|^{k}}\left\|c_{k}(p)-c_{k}(q)\right\|_{2}$

　　其中

• • $c_{k}$ 代表第 $k$ 阶中心矩，通常 $k=5$ ；
  • $a$、$b$ 表示这些分布的联合分布支持度；

　　上式值越大则两域距离越大。

　　本文定义的 GNNs 为  $H^{k}=\sigma\left(H^{k-1} \theta^{k}\right)$，传统的 GNNs 为 $H^{k}=\sigma\left(\tilde{A} H^{k-1} \theta^{k}\right)$。

　　传统的 GNNs 由于使用了归一化邻接矩阵，导致产生归纳偏差，从而改变了 表示的分布。所以在半监督学习中 ，由于 图归纳以及采样特征向量的偏移，有便宜的训练样本困难产生较大的性能干扰。

　　在形式上，对分布位移的分析如下：

　　Definition  3.1  (Distribution shift in GNNs). Assume node representations  $Z=\left\{z_{1}, z_{2}, \ldots, z_{n}\right\}$  are given as an output of the last hidden layer of a graph neural network on graph  $G$  with n nodes. Given labeled data  $\left\{\left(x_{i}, y_{i}\right)\right\}$  of size  $M$ , the labeled node representation  $Z_{l}=\left(z_{1}, \ldots, z_{m}\right)$  is a subset of the nodes that are labeled,  $Z_{l} \subset Z$ . Assume  $Z$  and  $Z_{l}$  are drawn from two probability distributions  $p$  and $q$. The distribution shift in GNNs is then measured via a distance metric  $d\left(Z, Z_{l}\right)$

　　Figure 1 表明样本偏差导致的分布偏移的影响直接降低了模型的性能。通过使用节点 GCN 模型绘制了三个数据集分布位移距离值( $x$ 轴)和相应的模型精度( $y$ 轴)的关系。

　　

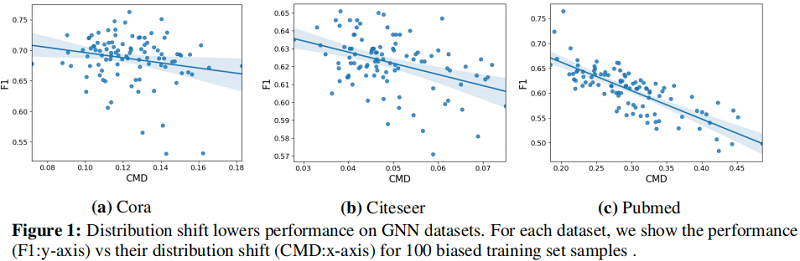
　　结果表明，GNN 在这些数据集上的节点分类性能与分布位移的大小成反比，并激发了我们对分布位移的研究。

4 Shift-Robust Graph Neural Networks

　　本节首先提出两种 GNN 模型解决分布位移问题（$\operatorname{Pr}_{\text {train }}(Z) \neq \operatorname{Pr}_{\text {test }}(Z)$，然后提出一种通用框架来减少分布位移2问题。

　　ben

　　ji

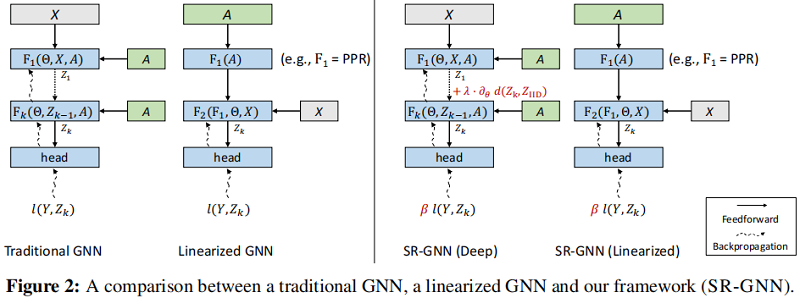
4.1 Scenario 1: Traditional GNN models

　　传统 GNN 模型 (GCN) $\Phi$ 包含 可学习函数 $\mathbf{F}$ ，参数 $\Theta$ ，邻接矩阵 $A$ :

　　　　$\Phi=\mathbf{F}(\Theta, A)$

　　在 GCN 中，图的归纳偏差在每一层上都是乘法的，并且梯度在所有层中反向传播。最后一层生成的节点表示为：

　　　　$Z \equiv Z_{k}=\Phi\left(\Theta, Z_{k-1}, A\right)$, $Z_{k} \in[a, b]^{n}$, $Z_{0}=X$

　　训练样本 $\left\{x_{i}\right\}_{i=1}^{M}$ 的节点表示为 $Z_{\text {train }}=\left\{z_{i}\right\}_{i=1}^{M}$。对于测试样本，从未标记的数据中抽取一个无偏的 IID 样本集 $X_{\text {IID }}=\left\{x_{i}^{\prime}\right\}_{i=1}^{M}$，并将输出表示为 $Z_{\text {IID }}=\left\{z_{i}^{\prime}\right\}_{i=1}^{M}$。

　　为减轻训练 和 测试样本之间的分布位移问题，本文提出一个正则化器 $d:[a, b]^{n} \times[a, b]^{n} \rightarrow \mathbb{R}^{+}$ 用于添加到交叉熵损失上。由于 $\Phi$ 是完全可微的，可以使用分布位移度量作为正则化，以直接最小化有偏和无偏的 IID 样本之间的差异：

　　　　$\mathcal{L}=\frac{1}{M} \sum_{i} l\left(y_{i}, z_{i}\right)+\lambda \cdot d\left(Z_{\text {train }}, Z_{\text {IID }}\right)$

　　这里度量分布位移采用 中心力矩差异正则化器（central moment discrepancy regularizer）$d_{\mathrm{CMD}}$：

　　　　$d_{\mathrm{CMD}}\left(Z_{\text {train }}, Z_{\mathrm{IID}}\right)=\frac{1}{b-a}\left\|\mathbf{E}\left(Z_{\text {train }}\right)-\mathbf{E}\left(Z_{\mathrm{IID}}\right)\right\|+\sum\limits_{k=2}^{\infty} \frac{1}{|b-a|^{k}}\left\|c_{k}\left(Z_{\text {train }}\right)-c_{k}\left(Z_{\mathrm{IID}}\right)\right\|$

　　其中，

• • $\mathbf{E}(Z)=\frac{1}{M} \sum_{i} z_{i}$；
  • $c_{k}(Z)=\mathbf{E}(Z-\mathbf{E}(Z))^{k}$ 是 $k$ 阶中心矩；

4.2 Scenario 2: Linearized GNN Models

　　线性化GNN模型使用两个不同的函数：一个用于非线性特征变换，另一个用于线性图扩展阶段：

　　　　$\Phi=\mathbf{F}_{\mathbf{2}}(\underbrace{\mathbf{F}_{\mathbf{1}}(\mathbf{A})}_{\text {linear function }}, \Theta, X)$

　　其中，线性函数 $\mathbf{F}_{\mathbf{1}}$ 将图归纳偏差与节点特征相结合，然后交予多层神经网络特征编码器 $\mathbf{F}_{\mathbf{2}}$ 解耦。SimpleGCN[34] 中 $\mathbf{F}_{\mathbf{1}}(A)=A^{k} X$ 。线性化模型的另一个分支 [16,4,36] 采用 personalized pagerank 来预先计算图中的信息扩散 ( $\mathbf{F}_{\mathbf{1}}(A)=\alpha(I-(1-\alpha) \tilde{A})^{-1}$ )，并将其应用于已编码的节点特性 $F(\Theta, X)$。

　　上述两种模型，图归纳偏差作为线性函数 $\mathbf{F}_{\mathbf{1}}$  的特征输入。但足够阶段并没有可学习层，所以不能简单使用上述提出的分布正则化器。

　　在这两种模型中，图归纳偏差作为线性 $\mathbf{F}_{\mathbf{1}}$ 的输入特征提供。不幸的是，由于在这些模型的这个阶段没有可学习的层，所以我们不能简单地应用前一节中提出的分布正则化器。

　　在这种情况下，可以将训练和测试样本视为来自 $\mathbf{F}_{\mathbf{1}}$ 的行级样本，然后将分布位移 $\operatorname{Pr}_{\text {train }}(Z) \neq \operatorname{Pr}_{\text {test }}(Z)$ 问题转化为匹配训练和测试图的归纳偏差特征空间 $h_{i} \in \mathbb{R}^{n}$。为从训练数据推广到测试数据，可以采用样本加权方案来纠正偏差，这样有偏差的训练样本 $\left\{h_{i}\right\}_{i=1}^{M}$ 将类似于IID样本 $ \left\{h_{i}^{\prime}\right\}_{i=1}^{M}$。由此得到的交叉熵损失为

　　　　$\mathcal{L}=\frac{1}{M} \beta_{i} l\left(y_{i}, \Phi\left(h_{i}\right)\right)$

　　其中，

• • $\beta_{i}$ 是每个训练实例的权值；
  • $l$ 是交叉熵损失；

　　然后，通过求解一个 核均值匹配(KMM)[9] 来计算最优 $\beta$：

　　　　$\min _{\beta_{i}}\left\|\frac{1}{M} \sum\limits_{i=1}^{M} \beta_{i} \psi\left(h_{i}\right)-\frac{1}{M^{\prime}} \sum\limits_{i=1}^{M^{\prime}} \psi\left(h_{i}^{\prime}\right)\right\|^{2} \text {, s.t. } B_{l} \leq \beta<B_{u}$

　　$\psi: \mathbb{R}^{n} \rightarrow \mathcal{H}$ 表示由核 $k$ 引入的 reproducing kernel Hilbert space(RKHS) 的特征映射。在实验中，作者使用混合高斯核函数 $k(x, y)=\sum_{\alpha_{i}} \exp \left(\alpha_{i}\|x-y\|_{2}\right)$, $\alpha_{i}=1,0.1,0.01 $。下限 $B_{l}$ 和上限 $B_{u}$ 约束的存在是为了确保大多数样本获得合理的权重，而不是只有少数样本 获得非零权重。

　　实际的标签空间中有多个类。为了防止 $\beta$ 引起的标签不平衡，进一步要求特定 $c$ 类的 $\beta$ 之和在 校正前后保持相同 $\sum_{i}^{M} \beta_{i} \cdot \mathbb{I}\left(l_{i}=c\right)=\sum_{i}^{M} \mathbb{I}\left(l_{i}=c\right), \forall c$ 。

4.3 Shift-Robust GNN Framework

　　现在我们提出了 Shift-Robust GNN(SR-GNN)-我们解决GNN中分布转移的一般训练目标：

　　　　$\mathcal{L}_{\text {SR-GNN }}=\frac{1}{M} \beta_{i} l\left(y_{i}, \Phi\left(x_{i}, A\right)\right)+\lambda \cdot d\left(Z_{\text {train }}, Z_{\text {IID }}\right)$

　　该框架由一个用于处理可学习层中的分布转移的正则化组件（第4.1节）和一个实例重加权组件组成，该组件能够处理在特征编码后添加了图归纳偏差的情况（第4.2节）。

　　现在，我们将讨论我们的框架的一个具体实例，并将该实例应用于APPNP[16]模型。APPNP模型的定义为：

　　　　$\Phi_{\text {APPNP }}=\underbrace{\left((1-\alpha)^{k} \tilde{A}^{k}+\alpha \sum\limits_{i=0}^{k-1}(1-\alpha)^{i} \tilde{A}^{i}\right)}_{\text {approximated personalized page rank }} \underbrace{\mathbf{F}(\Theta, X)}_{\text {feature encoder }}$

　　首先在节点特征 $X$ 上应用特征编码器 $\mathbf{F}$，并线性逼近 personalized pagerank matrix。因此，我们有 $h_{i}=\pi_{i}^{\mathrm{ppr}}$，其中 $\pi_{i}^{\mathrm{ppr}}$ 是个性化的页面向量。为此，我们通过实例加权来减轻由图归纳偏差产生的分布转移。此外，让 $Z=\mathbf{F}(\Theta, X)$ 和我们可以进一步减少非线性网络的分布位移提出的差异正则化器 $d$。在我们的实验中，我们展示了SR-GNN在另外两个具有代表性的GNN模型上的应用：GCN[15]和DGI[32]。

5 Experiments

实验

　　

　　

　　

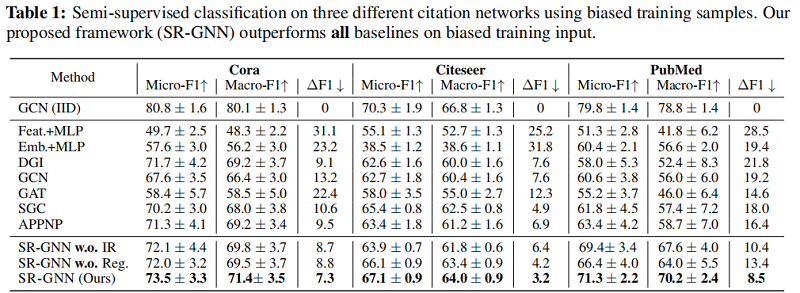
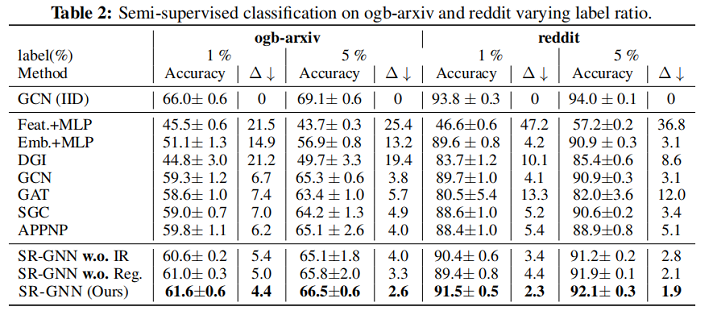
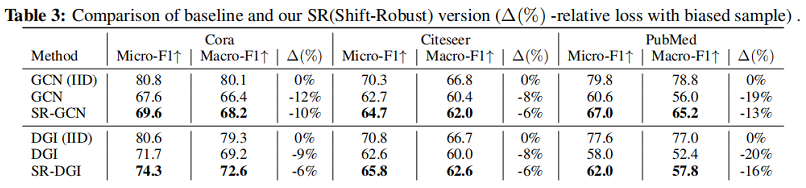
5 Conclusion

　　对于半监督学习，考虑表示分布一致性问题。

修改历史

2022-06-24 创建文章

论文解读目录