sklearn中的损失函数

python机器学习-乳腺癌细胞挖掘（博主亲自录制视频）

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

原文链接

https://www.cnblogs.com/nolonely/p/7008952.html

各种损失函数

损失函数或代价函数来度量给定的模型（一次）预测不一致的程度

损失函数的一般形式：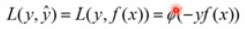

风险函数：度量平均意义下模型预测结果的好坏

损失函数分类：

Zero-one Loss，Square Loss，Hinge Loss，Logistic Loss，Log Loss或Cross-entropy Loss，hamming_loss

分类器中常用的损失函数：

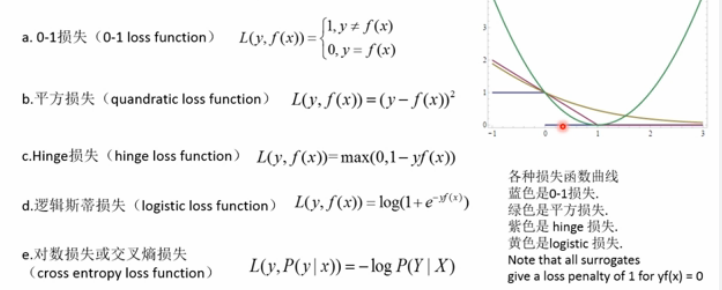
Zero-One Loss

该函数计算n_samples个样本上的0-1分类损失（L_0-1)的和或者平均值。默认情况下，返回的是所以样本上的损失的平均损失，把参数normalize设置为False，就可以返回损失值和

在多标签分类问题中，如果预测的标签子集和真实的标签子集严格匹配，zero_one_loss函数给出得分为1，如果没有任何的误差，得分为0

from sklearn.metrics import zero_one_loss
import numpy as np
#二分类问题
y_pred=[1,2,3,4]
y_true=[2,2,3,4]
print(zero_one_loss(y_true,y_pred))
print(zero_one_loss(y_true,y_pred,normalize=False))
#多分类标签问题
print(zero_one_loss(np.array([[0,1],[1,1]]),np.ones((2,2))))
print(zero_one_loss(np.array([[0,1],[1,1]]),np.ones((2,2)),normalize=False))

#结果：
#0.25
#1
#0.5
#1

Hinge Loss

该损失函数通常被用于最大间隔分类器，比如假定类标签+1和-1，y：是真正的类标签，w是decision_function输出的预测到的决策，这样，hinge loss 的定义如下：

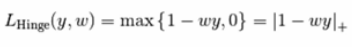
如果标签个数多于2个，hinge_loss函数依据如下方法计算：如果y_w是对真是类标签的预测，并且y_t是对所有其他类标签的预测里边的最大值，multiclass hinge loss定义如下：

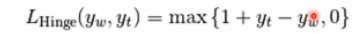
下面的代码展示了用hinge_loss函数度量SVM分类器在二元分类问题中的使用方法：

from sklearn import svm
from sklearn.metrics import hinge_loss
X=[[0],[1]]
y=[-1,1]
est=svm.LinearSVC(random_state=0)
print(est.fit(X,y))
pred_decision=est.decision_function([[-2],[3],[0.5]])
print(pred_decision)
print(hinge_loss([-1,1,1],pred_decision))

#结果
#LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
     intercept_scaling=1, loss='squared_hinge', max_iter=1000,
     multi_class='ovr', penalty='l2', random_state=0, tol=0.0001,
     verbose=0)
#[-2.18177262  2.36361684  0.09092211]
#0.303025963688

Log Loss（对数损失）或者Cross-entropy Loss（交叉熵损失）

在二分类时，真是标签集合为{0，1}，而分类器预测得到的概率分布为p=Pr（y=1）

每一个样本的对数损失就是在给定真是样本标签的条件下，分类器的负对数思然函数，如下所示：

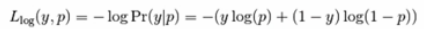
当某个样本的真实标签y=1时，Loss=-log（p），所以分类器的预测概率p=Pr（y=1）的概率越大，则损失越小；如果p=Pr（y=1）的概率越小，则分类损失就越大，对于真是标签y=0，Loss=-log（1-p），所以分类器的预测概率p=Pr（y=1）的概率越大，则损失越大

多分类跟这个类似，不在重复

　　

#Log Loss
from sklearn.metrics import log_loss
y_true=[0,0,1,1]
y_pred=[[0.9,0.1],[0.8,0.2],[0.3,0.7],[0.01,0.99]]
print(log_loss(y_true,y_pred))

#0.173807336691

Hamming Loss，计算两个样本集合之间的平均汉明距离

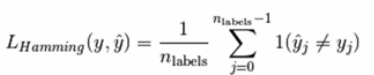
#hamming_loss
from sklearn.metrics import hamming_loss
y_pred=[1,2,3,4]
y_true=[2,2,3,4]
print(hamming_loss(y_true,y_pred))

#0.25

 https://study.163.com/provider/400000000398149/index.htm?share=2&shareId=400000000398149（ 欢迎关注博主主页，学习python视频资源，还有大量免费python经典文章）