决策单调性优化dp

决策单调性：

对于一些dp方程，经过一系列的猜想和证明，可以得出，所有取的最优解的转移点（即决策点）位置是单调递增的。

即：假设f[i]=min(f[j]+b[j]) (j<i) 并且，对于任意f[i]的决策点g[i]，总有f[i+1]的决策点g[i+1]>=g[i](或者<=g[i]) 那么，这个方程就具备决策单调性。

这个有什么用吗？

不懂具体优化方法的话确实也没有什么用。可能还是n^2的。只不过范围可能少了一些。

一

经典入门例题：

Description:

[POI2011]Lightning Conductor

已知一个长度为n的序列a1,a2,...,an。

对于每个1<=i<=n，找到最小的非负整数p满足 对于任意的j, aj < = ai + p - sqrt(abs(i-j))

Solution:

题目转化一下：就是对于每个i，找到aj+sqrt(abs(i-j))的最大值。

首先必须要先证明决策单调性：

当i>j时，即aj+sqrt(i-j)<=ai

假设对于i位置的决策点为g[i],那么对于任意的正数k，满足a[g[i]-k] + sqrt(i-g[i]+k) <= a[g[i]] + sqrt(i-g[i])

当i变成i+1 的时候， 因为幂函y = sqrt(x)是下凸的，

因为i-g[i]+k < i-g[i]

所以，sqrt(i+1-g[i]+k)-sqrt(i-g[i]+k) <  sqrt(i+1-g[i]) - sqrt(i-g[i]) （越大，加1越不明显）

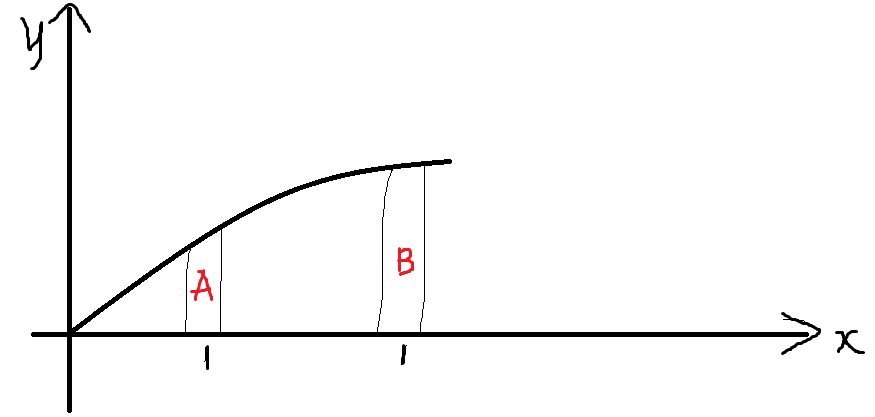
大概就是，A区域一段的增加幅度大于B区域一段。

所以：a[g[i]-k] + sqrt(i+1-g[i]+k) < a[g[i]] + sqrt(i+1-g[i])  不选的那个点更不优了。g[i+1]>=g[i] 所以有单调性。

当j>i 的时候，同理可证。

处理方法：

1.分治：

sol(l,r,L,R) 表示决策l，r这段区间，决策点可能在L，R。

每次取一个mid=（l+r）/2 , 暴力扫描L，R找到决策点id。分治到：sol(l,mid-1,L,id) 和 sol(mid+1,r, id,R)

因为对于>mid 的点，决策一定比id大。反过来同理。

logn层，每层扫描总共O(n) 复杂度nlogn

这个题用这个方法代码好写。

注意理解一下i<j和i>j的情况两次找。

#include<bits/stdc++.h>
using namespace std;
const int N=+;
double f[N][];
int a[N],n;
void sol(int l,int r,int L,int R,int ty){
    if(l>r) return;
    int mid=(l+r)>>;int id=;
    for(int i=L;i<=min(R,mid);i++){//注意，这里min(R,mid),每次只从前部分取max
        //保证了i<j或者i>j的前提下的决策单调性。(虽然看似都是j<i的单调性，但是我对称数组了呀)
        //可以根据题目样例画图理解一下
        if(1.0*a[i]+1.0*sqrt(1.0*abs(i-mid))>f[mid][ty]){
            f[mid][ty]=1.0*a[i]+1.0*sqrt(1.0*abs(i-mid));
            id=i;
        }
    }
    sol(l,mid-,L,id,ty);sol(mid+,r,id,R,ty);
}
int main()
{
    cin>>n;
    for(int i=;i<=n;i++) scanf("%d",&a[i]);
    sol(,n,,n,);
    for(int i=;i<=n/;i++) swap(a[i],a[n-i+]);//这里要对称一下，正反分别找一遍，
    //对应i<j和i>j的情况，这样决策才是一直单调的。
    sol(,n,,n,);
    for(int i=;i<=n;i++){
        int ans=(int)ceil(f[i][])-a[n-i+];
        int aa=(int)ceil(f[n-i+][])-a[n-i+];
        ans=max(ans,aa);
        printf("%d\n",ans);
    }
    return ;
}

缺陷在于：这个方法必须依赖于f[i]与之前的f们无关。因为先得出答案的是区间中间的值，没有任何顺序。

一般适用于二维dp —— SD_le

（因为，二维dp一般有f[i][k]=min(f[j][k-1]),f[j][k-1]们已经在之前算好了。就可以直接分治。不用考虑得出答案的顺序）

2.队列：

这个方法适用性比较普遍。

我们把思路转化一下，从考虑每个位置的决策点，到每个点是哪些位置的决策点。

根据决策单调性，这些位置一定是连续的一段区间。

从前到后1~n枚举i

每次枚举到i，就从队头取出最优解，更新答案。再用二分查找决策分界点。插入队尾。

具体解释：

维护一个队列，队列里存着三元组(id,l,r)，表示决策点和以id为最优决策点的区间(l,r)i从1扫到n
①i的最优决策点一定是队头的id，然后如果队头的r==i，弹出队头
②以i为最优决策点的区间一定是(x,n],然后从队列尾开始，如果队尾的q[tail].id在q[tail].l~q[tail].r中全劣于i，弹出队尾。
③当前队尾的元素在l~r中可能前一部分优于i，后一部分劣于i，二分这个分界点，修改q[tail].r
④如果q[tail].r!=n,将(i,q[tail].r+1,n)加入队尾
概括地说，1.取队头，2.判断弹队头 3.新决策点二分一个影响区间 4. 弹出队尾，或者弹出自己或者改变队尾区间影响范围。（5.加入自己）
不断循环3、4步，直到弹出自己或者改变范围。

循环当前的i，二分，nlogn

对于这个题，就是每次的i，找队头的id，更新f[i]，把自己加进去。

因为每次决策点都是之前的，所以也要对称数组再做一遍即可。

二

土地购买、玩具装箱也可以用决策单调性。

但是斜率优化毕竟O(n)更好。

三

[Lydsy1712月赛]小Q的书架

题面：https://www.lydsy.com/JudgeOnline/upload/201712/prob12.pdf

f[i][k]表示，前i个位置，在i后面砍第k刀的最小代价。

f[i][k]=min(f[j][k-1]+w(j+1,i)) j<i

w(l,r)即为l到r区间内的逆序对数量。

w显然满足四边形不等式。

用什么方法处理单调性呢？

发现，既然k从k-1转移，我们不妨从小到大枚举k

f[i][k-1]们都求出来了，所以可以直接分治。（毕竟分治好写）

至于w(l,r)

每次统计，就变成优秀的n^2logn“分治”了。

所以，用莫队思想。每次动一点。

复杂度肯定要优秀一些。但是不会证。。。

大概复杂度：
O(nksqrt(n)*logn+nlogn)实际莫队表现好像更快。

代码：

值得注意的是，R-L+1-query(a[R+1]-1)求区间多少个比a[R+1]大的。总的减去小的。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=+;
int n,m;
int f[N][];
int t[N];
int a[N];
void add(int x,int c){
    for(;x<=n;x+=x&(-x)) t[x]+=c;
}
int query(int x){int ret=;
    for(;x;x-=x&(-x)) ret+=t[x];
    return ret;
}
int ni;
int L,R;
void mov(int l,int r){
    //cout<<l<<" and "<<r<<endl;
    //cout<<L<<" ;; "<<R<<endl;
    while(R<r) ni+=(R-L+-query(a[R+]-)),add(a[++R],);
    while(L>l) ni+=query(a[L-]-),add(a[--L],);
    while(R>r) ni-=(R-L-query(a[R]-)),add(a[R--],-);
    while(L<l) ni-=query(a[L]-),add(a[L++],-);
}
void divi(int p,int l,int r,int L,int R){
    //cout<<p<<" "<<l<<" "<<r<<" : "<<L<<" "<<R<<endl;
    if(L>R) return;
    int mid=(L+R)/;
    int id=;
    for(int i=min(mid-,r);i>=l;i--){
        mov(i+,mid);
        //cout<<" jj"<<endl;
        if(f[i][p-]+ni<f[mid][p]){
            f[mid][p]=f[i][p-]+ni;
            id=i;
        }
    }
    divi(p,l,id,L,mid-);
    divi(p,id,r,mid+,R);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)scanf("%d",&a[i]);
    memset(f,0x3f,sizeof f);
    f[][]=;
    L=,R=;
    add(a[],);
    for(int k=;k<=m;k++){
        //cout<<" now "<<k<<endl;
        divi(k,,n-,,n);
    }
    printf("%d",f[n][m]);
    return ;
}

决策单调性感觉非常微妙，是的，微妙。

必须要往这方面去想。1e5数据范围

一般要通过推式子。（打表找规律）

---

证明单调性后，就比较套路了。