快速排序 java实现 (原理-优化) 三路快排
一、基本的快速排序
在数组中选取一个元素为基点,然后想办法把这个基点元素移动到它在排好序后的最终位置,使得新数组中在这个基点之前的元素都小于这个基点,而之后的元素都大于这个基点,然后再对前后两部分数组快速排序,直到数组排序完成。
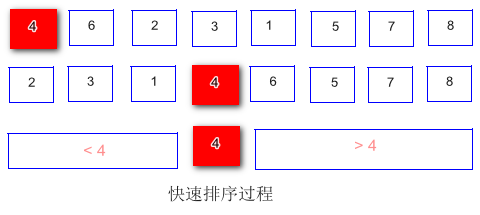
代码实现:
public void quickSorted ( int arr[] ) {
int n = arr.length - 1; // 闭区间 [0...n]
__quickSorted (arr, 0, n);
}
private __quickSorted( int arr[], int L, int R) {
if ( (L >= R) {
return;
}
// 将基点移动到最终位置的方法
int p = __partioner(arr, L, R);
// 递归拆分数组
__quickSorted(arr, L, p - 1);
__quickSorted(arr, p + 1, R);
}
那么最大的问题就是怎么把这个基点移动到它最终应该所在的位置。
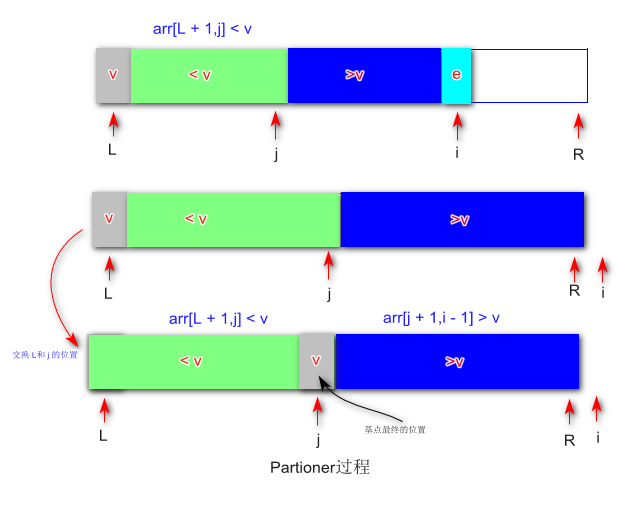
代码实现:
private int __partioner ( int arr[], int L, int R ) {
int v = arr[L];
// [L + 1, j] < v ; [j + 1, i) > v;
int j = L;
for ( int i = L + 1; i <= R; i++ ) {
if ( arr[i] < v) {
// 交换 arr[i] 和 arr [j + 1]
int tmp = arr[j + 1];
arr[j + 1] = arr[i];
arr[i] = tmp;
j++;
}
}
// 交换 arr[j] 和arr[L]
int tmp = arr[j];
arr[j] = arr[L];
arr[L] = tmp;
return j;
}
最终实现:
public void quickSorted ( int arr[] ) {
int n = arr.length - 1; // 闭区间 [0...n]
__quickSorted (arr, 0, n);
}
private __quickSorted( int arr[], int L, int R) {
if ( (L >= R) {
return;
}
// 将基点移动到最终位置的方法
int p = __partioner(arr, L, R);
// 递归拆分数组
__quickSorted(arr, L, p - 1);
__quickSorted(arr, p + 1, R);
}
private int __partioner ( int arr[], int L, int R ) {
int v = arr[L];
// [L + 1, j] < v ; [j + 1, i) > v;
int j = L;
for ( int i = L + 1; i <= R; i++ ) {
if ( arr[i] < v) {
// 交换 arr[i] 和 arr [j + 1]
int tmp = arr[j + 1];
arr[j + 1] = arr[i];
arr[i] = tmp;
j++;
}
}
// 交换 arr[j] 和arr[L]
int tmp = arr[j];
arr[j] = arr[L];
arr[L] = tmp;
return j;
}
快速排序完整代码
二、快速排序的优化
1. 快速排序的第一次优化,减小递归的深度,转而使用 选择排序
private __quickSorted( int arr[], int L, int R) {
// if ( (L >= R) {
// return;
// }
// 快速排序的第一次优化,减小递归的深度,转而使用 选择排序
if ( R - L <= 15) {
insertSorted(arr, L, R);
return;
}
// 将基点移动到最终位置的方法
int p = __partioner(arr, L, R);
// 递归拆分数组
__quickSorted(arr, L, p - 1);
__quickSorted(arr, p + 1, R);
}
// 减小递归的深度转而使用选择排序
private void insertSorted(int arr[], int L, int R) {
for (int i = L + 1; i <= R; i++) {
int i = arr[i];
int j;
for (j = i; j > L && arr[j - 1] > e; j--) {
arr[j] = arr[j - 1];
}
}
return;
}
2. 优化二,基点的选择随机化
private int __partioner ( int arr[], int L, int R ) {
// 第二次优化,将基点的选择随机化
int rand = (new Random().nextInt(R + 1)) + L;
// 交换最左侧和随机点的元素
int tmp = arr[rand];
arr[rand] = arr[L];
arr[L] = tmp;
int v = arr[L];
// [L + 1, j] < v ; [j + 1, i) > v;
int j = L;
for ( int i = L + 1; i <= R; i++ ) {
if ( arr[i] < v) {
// 交换 arr[i] 和 arr [j + 1]
int tmp = arr[j + 1];
arr[j + 1] = arr[i];
arr[i] = tmp;
j++;
}
}
// 交换 arr[j] 和arr[L]
int tmp = arr[j];
arr[j] = arr[L];
arr[L] = tmp;
return j;
}
三、两路快排
解决排序的数组中存在多数重复元素的情况
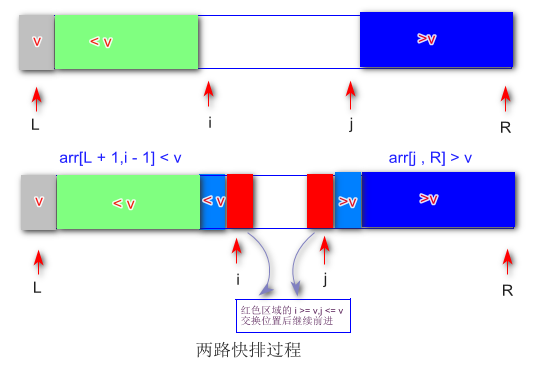
代码实现
public void quickSorted ( int arr[] ) {
int n = arr.length - 1; // 闭区间 [0...n]
__quickSorted (arr, 0, n);
}
private __quickSorted( int arr[], int L, int R) {
// if ( (L >= R) {
// return;
// }
// 快速排序的第一次优化,减小递归的深度,转而使用 选择排序
if ( R - L <= 15) {
insertSorted(arr, L, R);
return;
}
// 将基点移动到最终位置的方法
int p = __partioner(arr, L, R);
// 递归拆分数组
__quickSorted(arr, L, p - 1);
__quickSorted(arr, p + 1, R);
}
private int __partioner ( int arr[], int L, int R ) {
// 第二次优化,将基点的选择随机化
int rand = (new Random().nextInt(R + 1)) + L;
// 交换最左侧和随机点的元素
int tmp = arr[rand];
arr[rand] = arr[L];
arr[L] = tmp;
int v = arr[L];
// 两路快排的实现过程
int i = L + 1;
int j = R ;
while (true) {
while (i <= R && arr[i] < v ){
i++;
}
while (j >= L + 1 && arr[j] > v) {
j--;
}
if (i > j) {
break;
}
// 交换 i 和 j 的位置
int tmp arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
int tmp arr[L];
arr[L] = arr[j];
arr[j] = tmp;
return j;
}
// 减小递归的深度转而使用选择排序
private void insertSorted(int arr[], int L, int R) {
for (int i = L + 1; i <= R; i++) {
int i = arr[i];
int j;
for (j = i; j > L && arr[j - 1] > e; j--) {
arr[j] = arr[j - 1];
}
}
return;
}
两路快排代码实现
四、三路快排

代码实现:
public static void quickSorted3Ways(int arr[]) {
int n = arr.length -1;
// arr[0, n] 闭区间
__quickSorted3Ways(arr, 0, n);
}
private static void __quickSorted3Ways(int[] arr, int L, int R) {
// if (L >= R) {
// return;
// }
// 快速排序的第一次优化,减小递归的深度,转而使用 选择排序
if ( R - L <= 15) {
insertSorted(arr, L, R);
return;
}
// 第二次优化,将基点的选择随机化
int rand = (new Random().nextInt(R + 1)) + L;
// 交换最左侧和随机点的元素
int tmp = arr[rand];
arr[rand] = arr[L];
arr[L] = tmp;
int v = arr[L];
// partioner
// 这三个变量的初始值 , 相当重要
int lt = L; // arr[L + 1, lt] < v
int gt = R + 1; // arr[gt, R] > v
int i =L + 1; // arr[lt + 1, i ) ==v // 此处的 i 的比较对象
while (i < gt ) {
if (arr[i] < v) {
SortedHandler.swap(arr, i, lt + 1);
lt++;
i++;
} else if (arr[i] > v) {
SortedHandler.swap(arr, i, gt - 1);
gt--;
} else {
i++;
}
}
SortedHandler.swap(arr, lt, L);
__quickSorted3Ways(arr, L, lt -1);
__quickSorted3Ways(arr, gt, R);
}
三路快排
最后附上整篇 关于快速排序从实现到逐步优化的思路图 (画到我怀疑人生了....)
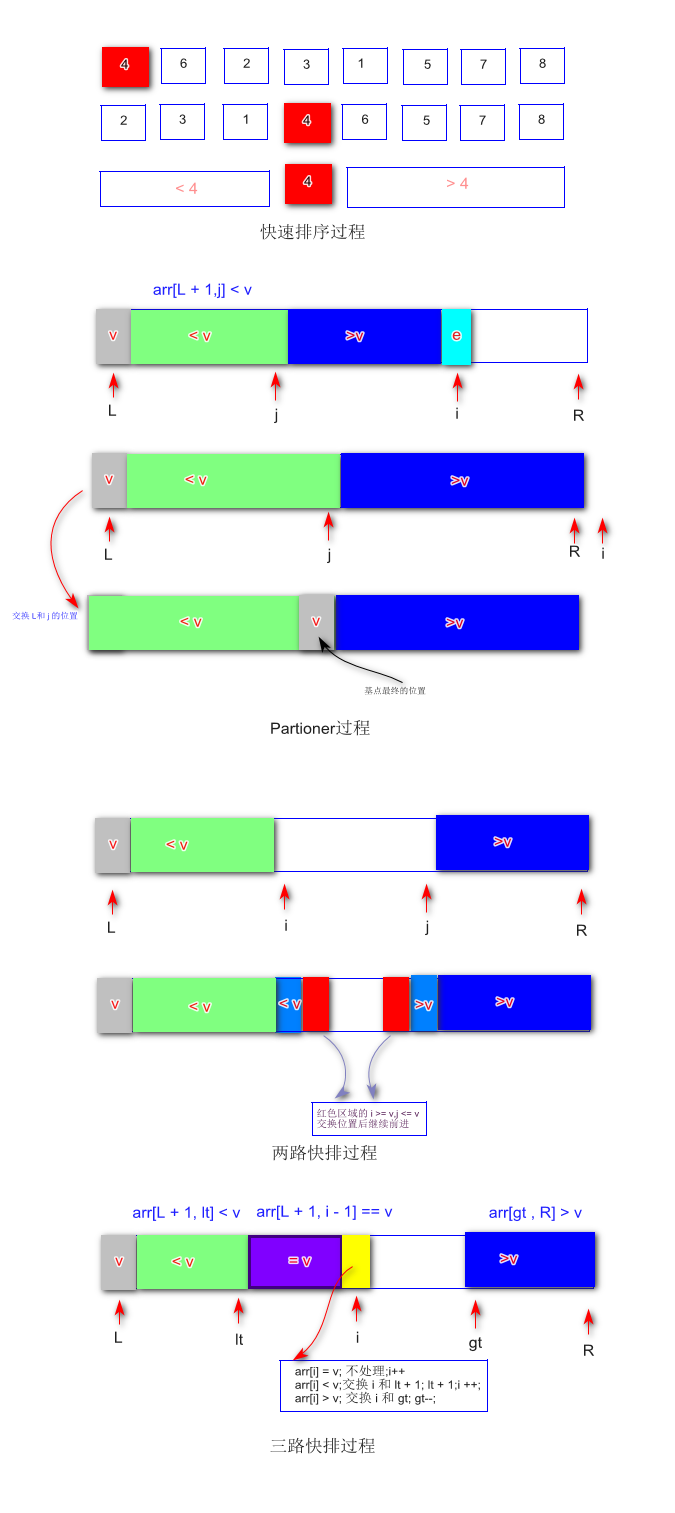
快速排序 java实现 (原理-优化) 三路快排的更多相关文章
- 快速排序—三路快排 vs 双基准
快速排序被公认为是本世纪最重要的算法之一,这已经不是什么新闻了.对很多语言来说是实际系统排序,包括在Java中的Arrays.sort. 那么快速排序有什么新进展呢? 好吧,就像我刚才提到的那样(Ja ...
- LeetCode 75. Sort Colors (颜色分类):三路快排
Given an array with n objects colored red, white or blue, sort them in-place so that objects of the ...
- 普林斯顿大学算法课 Algorithm Part I Week 3 重复元素排序 - 三路快排 Duplicate Keys
很多时候排序是为了对数据进行归类,这种排序重复值特别多 通过年龄统计人口 删除邮件列表里的重复邮件 通过大学对求职者进行排序 若使用普通的快排对重复数据进行排序,会造成N^2复杂度,但是归并排序和三路 ...
- leetcode 75 Sort Colors 计数排序,三路快排
解法一:计数排序:统计0,1,2 的个数 时间复杂度:O(n) 空间复杂度:O(k) k为元素的取值范围, 此题为O(1) class Solution { public: void sortC ...
- LeetCode 75. Sort Colors (python一次遍历,模拟三路快排)
LeetCode 75. Sort Colors (python一次遍历,模拟三路快排) 题目分析: 本题需要实现数字只包含0,1,2的排序,并且要求一次遍历. 由于只用把数字隔离开,很容易想到快排的 ...
- 【C语言编程入门笔记】排序算法之快速排序,一文轻松掌握快排!
排序算法一直是c语言重点,各个算法适应不用的环境,同时,在面试时,排序算法也是经常被问到的.今天我们介绍下快速排序,简称就是快排. 1.快速排序思想: 快排使用 分治法 (Divide and con ...
- Java写 插入 选择 冒泡 快排
/** * Created by wushuang on 2014/11/19. */ public class SortTest { @Test public void mainTest() { i ...
- <泛> 多路快排
今天写一个多路快排函数模板,与STL容器兼容的. 我们默认为升序排序 因为,STL容器均为逾尾容器,所以我们这里采用的参数也是逾尾的参数 一.二路快排 基本思路 给你一个序列,先选择一个数作为基数,我 ...
- LeetCode75----分类颜色(变相快排)
给定一个包含红色.白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色.白色.蓝色顺序排列. 此题中,我们使用整数 0. 1 和 2 分别表示红色.白色和蓝色. ...
随机推荐
- 从零开始构建一个的asp.net Core 项目(一)
最近突发奇想,想从零开始构建一个Core的MVC项目,于是开始了构建过程. 首先我们添加一个空的CORE下的MVC项目,创建完成之后我们运行一下(Ctrl +F5).我们会在页面上看到“Hello W ...
- RESTFUL 概念
1. 什么是REST REST全称是Representational State Transfer,中文意思是表述(编者注:通常译为表征)性状态转移. 它首次出现在2000年Roy Fielding的 ...
- IOS数据持久化存储之SQLite3第三方库FMDB的使用
SQLite是一种小型的轻量级的关系型数据库,在移动设备上使用是非常好的选择,无论是Android还是IOS,都内置了SQLite数据库,现在的版本都是SQLite3.在IOS中使用SQLite如果使 ...
- ubuntu 下安装nanomsg和nnpy
nanomsg nanomsg是ZeroMQ作者用C语言重写的一个Socket库,其用法和模式和ZeroMQ差不多,但是具有更好的性能和更完善的接口. 首先下载源码 wget https://gith ...
- Python OrderedDict使用
一.最近最少使用实现: import collections class LRUDict(object): ''' 最近最少使用队列实现,最近使用的键值放后面 ''' def __init__(sel ...
- Texture Combiner
[Texture Combiner] After the basic vertex lighting has been calculated, textures are applied. In Sha ...
- sourcetree免注册方法
step1: https://www.sourcetreeapp.com/官网下载windows版软件 step2: 右键-->以管理员身份运行,便安装成功了 step3: 安装好之后会有这么一 ...
- CCScrollView练习
MyScrollItem是CCScrollView容器内项的接口,MyScrollView主要处理添加子节点和事件的处理,MyScrollViewTestItem是对MyScrollItem实现的测试 ...
- 添加字段modify
ALTER TABLE tc_activity_turntable ADD `foot_pic` VARCHAR () NOT NULL DEFAULT '' COMMENT '底部图片';
- [SoapUI] Global Scripts For Reusability
