2013长春网赛1009 hdu 4767 Bell（矩阵快速幂+中国剩余定理）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4767

题意：求集合{1, 2, 3, ..., n}有多少种划分情况bell[n]，最后结果bell[n] mod 95041567.

分析：首先了解三个概念：贝尔数   第二类斯特灵数   中国剩余定理

贝尔数是指基数为n的集合的划分方法的数目。

贝尔数适合递推公式：

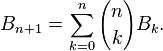
每个贝尔数都是"第二类Stirling数"的和

贝尔数满足两个公式：（p为质数）

            1) B[n+p] = B[n] + B[n+1] （mod p） ;

            2) B[p^m+n] = m*B[n] + B[n+1] （mod p） .

将95041567质因数分解发现，95041567 = 31*37*41*43*47

所以B[n]%95041567可以分解为 B[n]%p(p=31,41,43,47)，

我们可以先求出B[n] mod p[i]的值a[i],这样问题就转化为 X=a[i](mod p[i])，

很明显这是几个一次同余方程，最后用中国剩余定理合并就可以了。

那要怎么求B[n]%p[i]呢？

利用上面的公式（1），我们发现这是 一个递推式，所以可以利用矩阵法来求解。

我们可以构造一个大小为当前p*p的矩阵。

这样我们就可以求出任意的B[n]了

我们可以先用贝尔数递推公式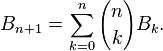求出前50个贝尔数，因为p[i]<50，所以对于大于p[i]的贝尔数，由上面的矩阵法可以求得。

比如：| 1 1 0 0 .... 0 0 |      |   B[1]  |      | B[1+p] |

| 0 1 1 0 .... 0 0 |      |   B[2]  |      | B[2+p] |

| 0 0 1 1 .... 0 0 |      |   B[3]  |      | B[3+p] |

| ....  .... .... ....  |  *  |   .....   |  =  |    .....   |

| 0 0 0 0 .... 1 1 |      | B[p-1] |      | B[2p-1]|

| 1 1 0 0 .... 0 1 |      |   B[p]  |      | B[2p]   |

若n=i+p,则只需求一次A*C=D，然后输出D[n-p]即D[i]就行了，

比如p[0]=31，如要求B[32]=B[1+31]，只需求一次A*C=D,然后输出D[1]，求B[51]则输出D[20]。

那么

若n=i+p^m,这只需求A^m*C=D，然后输出D[i]即可

到此算法结束

总结一下：

先用贝尔数递推公式求出前50个贝尔数，然后用矩阵快速幂分别求出bell[n]%p[i]赋给a[i]，然后用中国剩余定理合并结果就可以求出bell[n]%95041567了。

AC代码如下：

 #include<stdio.h>
 #include<string.h>
 #define LL __int64
 int w[]={,,,,};
 LL c[][][],bell[][];
 LL a[];
 struct Matrix{
     LL m[][];
 };
 void init()
 {
     int i,j,k;
     for(k=;k<;k++)
     {
         c[][][k]=;
         for(i=;i<;i++)     //c[i][j][k] 表示c(i,j)%w[k]
         {
             c[i][][k]=c[i][i][k]=;
             for(j=;j<i;j++)
                 c[i][j][k]=(c[i-][j-][k]+c[i-][j][k])%w[k];
         }
     }
     // 预处理出前50项分别取模的大小
     for(k=;k<;k++)
     {
         bell[][k]=;
         for(i=;i<;i++)
         {
             bell[i][k]=;
             for(j=;j<i;j++)
             {
                 bell[i][k]=(bell[i][k]+c[i-][j][k]*bell[j][k])%w[k];
             }
         }
     }
 }
 LL exgcd(LL a,LL b,LL &x,LL &y)    //扩展欧几里得
 {
     if(b==)
     {
         x=; y=;
         return a;
     }
     LL d=exgcd(b,a%b,x,y);
     LL t=x;
     x=y;
     y=t-a/b*y;
     return d;
 }
 LL CRT(int k)     //中国剩余定理
 {
     LL i,N=,ans=;
     LL t,x,y,d;
     for(i=;i<k;i++)
         N*=w[i];
     for(i=;i<k;i++)
     {
         t=N/w[i];
         d=exgcd(t,w[i],x,y);
         ans=(ans+x*t*a[i])%N;
     }
     return (ans+N)%N;
 }
 Matrix mul(Matrix x,Matrix y,int n,int mod)      //矩阵乘法
 {
     int i,j,k;
     Matrix tmp;
     memset(tmp.m,,sizeof(tmp.m));
     for(i=;i<=n;i++)
         for(j=;j<=n;j++)
             for(k=;k<=n;k++)
             {
                 tmp.m[i][j]+=(x.m[i][k]*y.m[k][j])%mod;
                 tmp.m[i][j]%=mod;
             }
     return tmp;
 }
 Matrix quickpow(Matrix res,Matrix A,int k,int n,int mod)   //矩阵快速幂模
 {
     int i;
     memset(res.m,,sizeof(res.m));
     for(i=;i<=n;i++)
         res.m[i][i]=;
     while(k)
     {
         if(k&)
             res=mul(res,A,n,mod);
         A=mul(A,A,n,mod);
         k>>=;
     }
     return res;
 }
 LL BellNumber(int n,int p)    //求bell[n][p]即bell[n]%w[p]
 {
     int i;
     if(n<)
         return bell[n][p];
     Matrix A,origin,ans;
     memset(A.m,,sizeof(A.m));
     memset(origin.m,,sizeof(origin.m));
     for(i=;i<w[p];i++)
         A.m[i][i]=A.m[i][i+]=;
     A.m[w[p]][]=;
     A.m[w[p]][]=;
     A.m[w[p]][w[p]]=;
     for(i=;i<=w[p];i++)
         origin.m[i][]=bell[i][p];
     LL cnt=n/w[p];
     n=n-w[p]*cnt;
     Matrix res;
     res=quickpow(res,A,cnt,w[p],w[p]);
     ans=mul(res,origin,w[p],w[p]);
     return ans.m[n][];
 }
 void solve(int n)
 {
     int i;
     for(i=;i<;i++)
         a[i]=BellNumber(n,i);    //bell[n]mod各个质数的值
     LL ans=CRT();
     printf("%I64d\n",ans);
 }
 int main()
 {
     int t,n;
     init();
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d",&n);
         solve(n);
     }
     return ;
 }