受限玻尔兹曼机（RBM）以及对比散度（CD）

1. RBM 的提出

BM 的缺点：

• 计算时间漫长，尤其是无约束自由迭代的负向阶段；
• 对抽样噪音敏感；
• 流行软件的不支持；

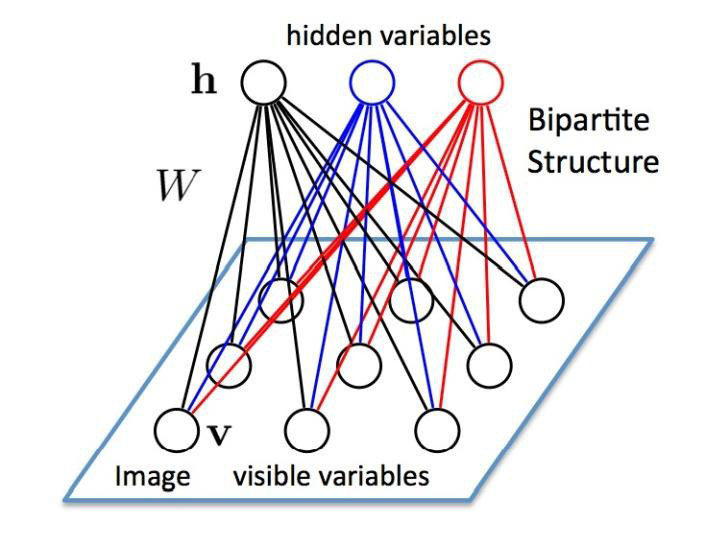
受限玻尔兹曼机（Restricted Boltzmann Machine,简称 RBM，以解决 BM 的学习效率过慢的严重缺陷）是由 Hinton 和 Sejnowski 于 1986 年提出的一种生成式随机神经网络（generative stochastic neural network），该网络由一些可见单元(visible unit，对应可见变量，亦即数据样本)和一些隐藏单元(hidden unit，对应隐藏变量)构成，可见变量和隐藏变量都是二元变量，亦即其状态取{0,1}。整个网络是一个二部图，只有可见单元和隐藏单元之间才会存在边，可见单元之间以及隐藏单元之间都不会有边连接，如下图所示：

2. BM 与 RBM 的对比

• RBM 和 BM 一样，都可视为一种无向图（undirected graph），所谓无向的涵义即在于，权值对称，wji=wij（自然对于有向图而言，与指向有关；）

• RBM 同层节点之间没有连接（BM 有连接），

  • 可见层，隐层：结点之间彼此独立（简化的思路）（条件独立假设），

3. 数学记号

• 能量函数的定义：

  E(v,h|θ)=−∑iaivi−∑jbjhj−∑in∑jmaiWijbj
  • 显然可以将上述公式简化为：一种向量的记法；
  • ai：可见层的偏置（bias）
  • bj：隐层的偏置（bias）
  • 竖线右边的 θ 就像条件概率的形式一样，一般理解为固定 θ（θ={Wij,ai,bj}）的条件下，E 关于 v,h 的函数；

• v,h 的联合概率分布为（由玻尔兹曼分布而来）：

  P(v,h)=e−E(v,h|θ)Z(θ)

  Z 十分难计算（2n+m 种组合）

4. CD 算法

θ∗=argmaxL(θ)=argmax∑t=1TlogP(v(t)|θ)

目标函数，即在参数（θ）确定的情况，最大化重现（再现）输入；

5. AE 与 RBM

• AE：
  • 出于简化的考虑：输入层，隐层，输出层；
  • 因为通过低维的隐层，可以重构出输出层，可见低维的隐层，是一种对输入本质特征的描述，又可从侧面说明，输入层是可以被压缩，也即存在冗余，进一步我们可认为其是可以被稀疏表示的；
    
    • 平方损失，BP反向传播，
• RBM：
  
  • 可见层，隐层，可见层，隐层 ,,, ，是一种横向的展开；
  • 这种周期性的循环结构可以被视为：不同的可见层其实是相互重叠的；
  • 可见层既作为输入，也作为输出，（之所以称其为可见层，隐层，而不是输入层，隐层，输出层，就在于，可见层既作为输入层，也作为输出层）

  -