Matlab 编程简介与实例

函数作图

二维平面曲线作图函数 plot(x, y, 's')

x, y是长度相同的向量，s表示线型和颜色

如果作多条曲线在同一图上，则用函数：

plot(x1, y1, 's1', x2, y2, 's', ... , xn, yn, 'sn')

代码如下：

效果如下：

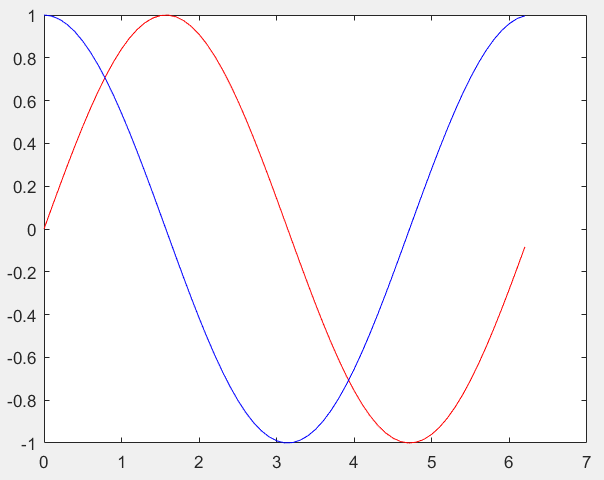
多窗口作图：

将屏幕分为几个窗口分别作图

subplot(m, n, k) 表示将窗口分为m * n个

当前图在第 k 个窗口完成

grid on 画上网格线

效果如下：

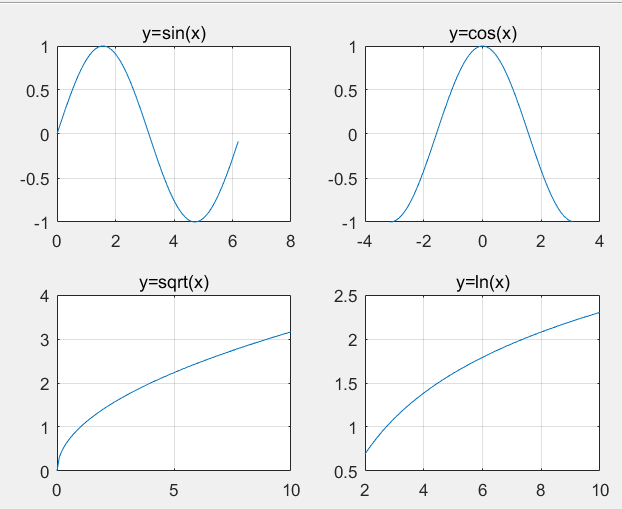
直方图作图 hist

二维直方图，可以显示数据的分布

count = hist(x) 把向量 x 中的元素放入等距的10个条形中，且返回每一个条形中的元素个数

count = hist(x， center) 参量 x 为向量，把 x 中元素放到 m (m = length(center)) 个由 center 中元素指定的位置为中心的直方图中。

count = hist(x, number) 参量 number 为标量，用于指定条形的数目。

[count, center] = hist(x) 返回向量 x 中包含频率计数的 count 与条形的位置向量 center，可以用命令 bar(center, count) 画出条形直方图。

如作1000个服从正态分布N(10, 25)数据的直方图：

代码如下：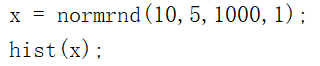

效果如下：

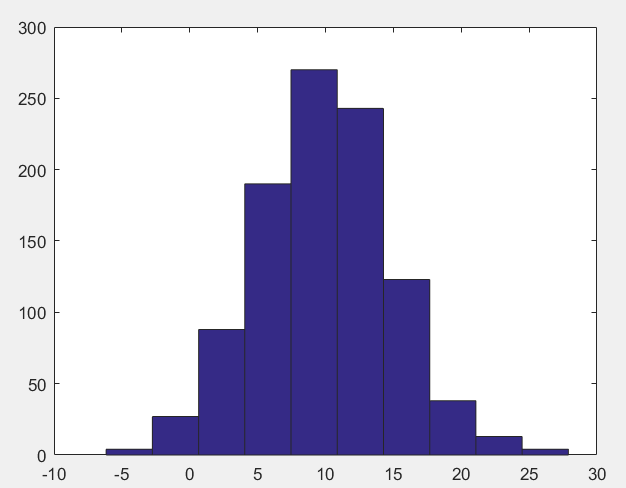
代码如下：

效果如下：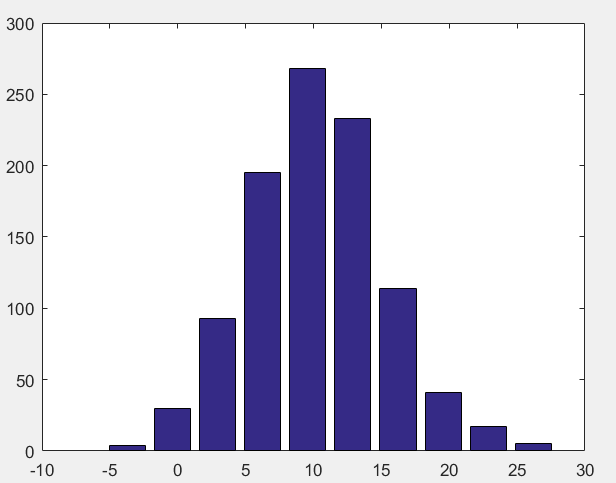

二维图形注释命令 grid

grid on 给当前的坐标轴增加分割线

grid off 从当前的坐标轴中去掉分割线

grid 转换分割线的显示与否的状态

grid(axes_handle, on | off) 对指定的坐标轴 axes_handle 是否显示分割线

空间曲线作图

三维曲线作图 plot3: plot(x, y, z, 's')

x, y 和 z 是长度相同的向量，s 表示线型和颜色

例如作空间螺旋线：

效果如下：

mesh命令

生成由x，y 和 z 指定的网线面，用法：mesh(x, y, z) 画出三维网格图

如作z = cosx . siny曲面图

代码如下：

效果如下：

surf 命令

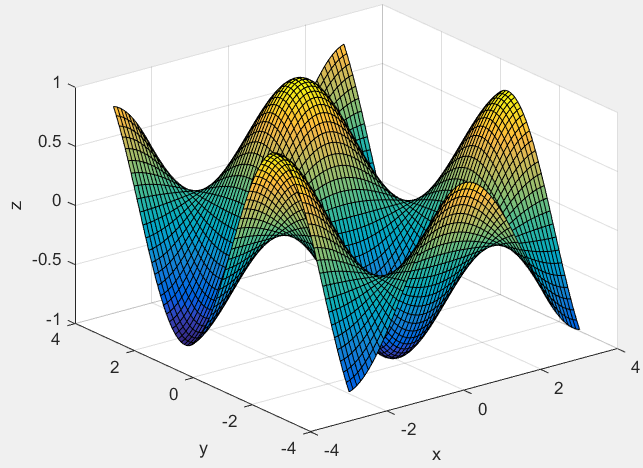
surf(x, y, z) 在矩形区域内显示三维带阴影曲面图

效果如下：

基本语句：

for 语句（已知循环次数）

求1+3+5+......+99

2 为步长，如果不写，默认为1

while 语句（未知循环次数，但知结束条件）

求1+3+5+......+99

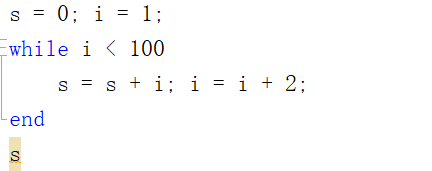
if 语句

分为单分支、双分支、多分支，看情况选择

求1到100中被3整除余1的数和为s1，被3整除余2的数和为s2，被3整除的数和为s3

代码如下：

输出如下：

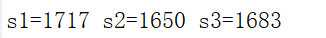
M 文件

M 文件有两种，一种是脚本 M 文件和函数 M 文件

函数 M 文件的第一行必须以一特殊字符 function 开始，格式为：function 因变量名=函数名(自变量名)

函数 M 文件和脚本 M 文件的差异:：

函数 M 文件的文件名必须与函数名相同，脚本 M 文件则可以任意取合法的名字。
脚本 M 文件没有输入参数与输出参数，而函数 M 文件有输入与输出参数，对函数进行调用时，可以按少于函数 M 文件规定的输入与输出变量个数，但不能多于函数 M 文件规定的输入与输出变量个数。
脚本 M 文件运行产生的所有变量都是全局变量，而函数 M 文件的所有变量除特别声明外都是局部变量。

如计算函数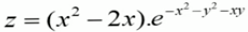在（0.1, 0.2）处的函数值

编写 M 文件 fun.m

调用：