点分治——POJ 1741

写的第一道点分治的题目，权当认识点分治了。

点分治，就是对每条过某个点的路径进行考虑，若路径不经过此点，则可以对其子树进行考虑。

具体可以看menci的blog:点分治

来看一道例题:POJ 1741 Tree

题目大意：扔给你一颗有权无根树，求有多少条路径的长度小于k；

解题思路：先找出重心，用一次dfs处理出每个点到根的距离dis，然后将dis[]排序，用O(n)的复杂度处理出"过根且长度小于等于k的路径数目"，删除根节点，对于每棵子树重复上述操作。

注意要去重：

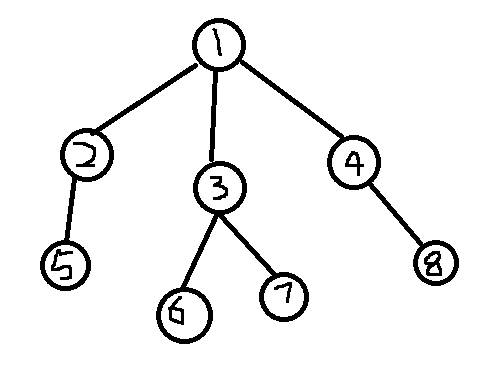
像上面这样一个图，假设每条边的长度为1，即点到根的路径长等于点的深度，设k=4。此时dis[6]=2,dis[7]=2;dis[6]+dis[7]=4=k。但是当分治以③为根节点的子树时，dis[6]+dis[7]=2<k，这样6->7这条路径就被计算了两次，所以每次求完过根节点的符合条件的路径数之后，要减去在同一棵子树下的节点之间的符合条件的路径数。

代码：

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 using namespace std;

 struct edge{
     int to,next,w;
 }e[];

 int root,ans,u,v,l,n,kk,ne,size;
 int head[],s[],d[],dis[],f[];
 //s[k]为k的子节点数目，dis[k]为k到根节点的距离
 bool b[];

 void add(int a,int b,int c){
     e[++ne].to=b; e[ne].w=c; e[ne].next=head[a]; head[a]=ne;
 }

 void getroot(int k,int fa){
     int v,i;
     s[k]=;
     f[k]=;
     for(i=head[k];i!=-;i=e[i].next){
         v=e[i].to;
         if(v!=fa&&!b[v]){
             getroot(v,k);
             s[k]+=s[v];//递归求子节点数目
             f[k]=max(f[k],s[v]);
         }
     }
     f[k]=max(f[k],size-s[k]);//dp求重心
     if(f[k]<f[root])root=k;
 }

 void getdis(int k,int fa){
     int i,v;
     d[++d[]]=dis[k];//储存距离以便排序
     for(i=head[k];i!=-;i=e[i].next){
         v=e[i].to;
         if(v!=fa&&!b[v]){
             dis[v]=dis[k]+e[i].w;//dfs求距离
             getdis(v,k);
         }
     }
 }

 int clac(int k,int init){
     int i,j,ret=;
     d[]=;
     dis[k]=init;
     getdis(k,);
     sort(d+,d++d[]);
     for(i=,j=d[];i<j;)
         if(d[i]+d[j]<=kk)ret+=j-i++;//计算路径数
         else j--;
     return ret;
 }

 void work(int k){
     int v,i;
     ans+=clac(k,);//计算路径数并加在ans上
     b[k]=true;//标记重心为删除
     for(i=head[k];i!=-;i=e[i].next){
         v=e[i].to;
         if(!b[v]){
             ans-=clac(v,e[i].w);//去重
             f[]=size=s[v];
             getroot(v,root=);//更新重心
             work(root);//对子树求解
         }
     }
 }

 int main(){
     int i;
     while(scanf("%d%d",&n,&kk)==){
         if(n==&&kk==)break;
         for(i=;i<=n;i++){
             head[i]=-;
             b[i]=;
         }
         ne=;
         for(i=;i<=n-;i++){
             scanf("%d%d%d",&u,&v,&l);
             add(u,v,l);
             add(v,u,l);//注意要连双向边
         }
         root=;
         f[]=size=n;
         getroot(,);//求重心
         ans=;
         work(root);
         printf("%d\n",ans);
     }
     return ;
 }

总体上感觉点分治不是很难理解，只要对题目有思路应该能写出来。（orz就是写代码经常出错!b[v]写成!b[k]之类的还查不出来）