LCA+树状数组 POJ 2763 Housewife Wind

题目传送门

题意：两种操作，问u到v的距离，并且u走到了v；把第i条边距离改成w

分析：根据DFS访问顺序，将树处理成链状的，那么回边处理成负权值，那么LCA加上BIT能够知道u到v的距离，BIT存储每条边的信息，这样第二种操作也能用BIT快速解决

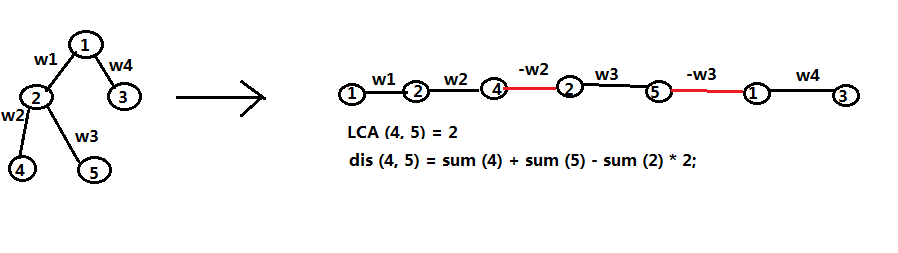
利用RMQ的写法不知哪里写挫了，改用倍增法

/************************************************
* Author        :Running_Time
* Created Time  :2015/10/6 星期二 11:45:03
* File Name     :POJ_2763.cpp
 ************************************************/

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cstring>
#include <cmath>
#include <string>
#include <vector>
#include <queue>
#include <deque>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <bitset>
#include <cstdlib>
#include <ctime>
using namespace std;
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
typedef long long ll;
const int N = 1e5 + 10;
const int D = 20;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const double EPS = 1e-8;
struct Edge {
    int v, w, id, nex;
}edge[N<<1];
struct BIT  {
    int c[N<<1], NN;
    void init(int n) {
        NN = n * 2;
        memset (c, 0, sizeof (c));
    }
    void updata(int i, int x)   {
        while (i <= NN) {
            c[i] += x;  i += i & (-i);
        }
    }
    int query(int i)    {
        int ret = 0;
        while (i)   {
            ret += c[i];    i -= i & (-i);
        }
        return ret;
    }
}bit;
int head[N];
int dep[N], rt[D][N], id[N], in[N], out[N];
int cost[N];
int e, tim;

void init(void) {
    memset (head, -1, sizeof (head));
    e = 0;
}

void add_edge(int u, int v, int w, int id)  {
    edge[e] = (Edge) {v, w, id, head[u]};
    head[u] = e++;
}

void DFS(int u, int fa, int d) {
    dep[u] = d; rt[0][u] = fa;
    for (int i=head[u]; ~i; i=edge[i].nex)  {
        Edge &e = edge[i];
        if (e.v == fa)  continue;
        in[e.id] = id[e.v] = ++tim;
        DFS (e.v, u, d + 1);
        out[e.id] = ++tim;
    }
}

int LCA(int u, int v)   {
    if (dep[u] < dep[v])    {
        swap (u, v);
    }
    for (int i=0; i<D; ++i) {
        if ((dep[u] - dep[v]) >> i & 1) {
            u = rt[i][u];
        }
    }
    if (u == v) return u;
    for (int i=D-1; i>=0; --i)  {
        if (rt[i][u] != rt[i][v])   {
            u = rt[i][u];
            v = rt[i][v];
        }
    }
    return rt[0][u];
}

int main(void)    {
    int n, q, s;
    while (scanf ("%d%d%d", &n, &q, &s) == 3)   {
        init ();
        for (int u, v, w, i=1; i<n; ++i)    {
            scanf ("%d%d%d", &u, &v, &cost[i]);
            add_edge (u, v, cost[i], i);
            add_edge (v, u, cost[i], i);
        }
        tim = 0;
        DFS (1, -1, 0);
        for (int i=1; i<D; ++i) {
            for (int j=1; j<=n; ++j)    {
                rt[i][j] = rt[i-1][j] == -1 ? -1 : rt[i-1][rt[i-1][j]];
            }
        }

        bit.init (n);
        for (int i=1; i<n; ++i) {
            bit.updata (in[i], cost[i]);        //入边序号
            bit.updata (out[i], -cost[i]);      //回边序号
        }

        int u = s;
        for (int op, i=1; i<=q; ++i)    {
            scanf ("%d", &op);
            if (op == 0)    {
                int v;  scanf ("%d", &v);               //入点序号和回点序号
                printf ("%d\n", bit.query (id[u]) + bit.query (id[v]) - bit.query (id[LCA (u, v)]) * 2);
                u = v;
            }
            else    {
                int p, w;   scanf ("%d%d", &p, &w);
                bit.updata (in[p], w - cost[p]);
                bit.updata (out[p], cost[p] - w);
                cost[p] = w;
            }
        }
    }   

    return 0;
}