【NOIP2006】作业调度方案 {语文难题}

Description:

　　我们现在要利用 m 台机器加工 n 个工件，每个工件都有 m 道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。 
　　每个工件的每个工序称为一个操作，我们用记号 j-k 表示一个操作，其中 j 为 1 到 n 中的某个数字，为工件号； k 为 1 到 m 中的某个数字，为工序号，例如 2-4 表示第 2 个工件第 4 道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。 
　　例如，当 n=3 ， m=2 时，“ 1-1 ， 1-2 ， 2-1 ， 3-1 ， 3-2 ， 2 -2 ” 就是一个给定的安排顺序，即先安排第 1 个工件的第 1 个工序，再安排第 1 个工件的第 2 个工序，然后再安排第 2 个工件的第 1 个工序，等等。 
　　一方面，每个操作的安排都要满足以下的两个约束条件。 
　　(1) 对同一个工件，每道工序必须在它前面的工序完成后才能开始； 
　　(2) 同一时刻每一台机器至多只能加工一个工件。 
　　另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。 
　　由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为“ 1 1 2 3 3 2 ” 。 
　　还要注意，“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。 
　　例如，取 n=3,m=2 ，已知数据如下：

　　

　　当一个操作插入到某台机器的某个空档时（机器上最后的尚未安排操作的部分也可以看作一个空档），可以靠前插入，也可以靠后或居中插入。为了使问题简单一些， 我们约定：在保证约束条件（ 1 ）（ 2 ）的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件（ 1 ）（ 2 ）的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。 
　　显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。

solution:

　　这道题完全是在考语文水平啊,数据范围都异常的小!然而我还是被坑了!

　　首先是题目描述本来就模模糊糊的,这道题是说按照顺序一个一个的去考虑他所给出的顺序的工件,按照要求放入队列,但是放入队列的时候要注意很多

　　例如:

• 1,2,3,4号工件先后放入,都是放入第一台机器.
• 然后再放入4,放入第二台机器.

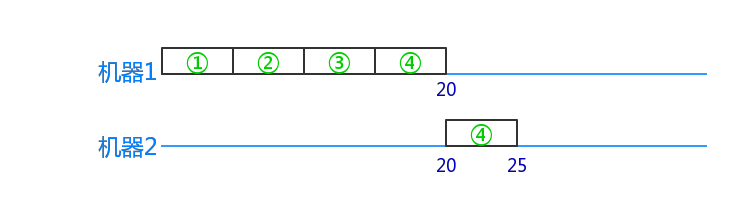
• 假设第一台机器已经占用了时间20s,那么第二台机器的4号工件必须从20s开始(同一个工件要按照工序去生产).
• 那么1~20s就是空余的.
• 如果再插入一个1号工件在2号机器,那么就要插到4号前面去了,即使与它给的顺序不同.

codes:

 #include<queue>
 #include<cstdio>
 #include<vector>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #define RG register
 using namespace std;
 int n,m,top,ans;
 int Time[][],mach[][],tot[];
 int que[],Rank[],Lasttime[];
 bool work[][];
 bool check(int Begin,int T,int id)
 {
   for(int i=Begin;i<Begin+T;i++)
     if(work[id][i])
       return ;
   return ;
 }
 int main()
 {
   scanf("%d%d",&m,&n);
   top=n*m;
   for(int i=;i<=top;i++)
     {
       scanf("%d",&que[i]);
       tot[que[i]]++;
       Rank[i]=tot[que[i]];
     }
   for(int i=;i<=n;i++)for(int j=;j<=m;j++)scanf("%d",&mach[i][j]);
   for(int i=;i<=n;i++)for(int j=;j<=m;j++)scanf("%d",&Time[i][j]);
   for(int j=,i;j<=top;j++)
     {
       int now=que[j];//当前的工件号
       int id=mach[now][Rank[j]];//当前的工序的机器号
       for(i=Lasttime[now]+;;i++)
     {
       if(!work[id][i])//检查是否可以插入任务
         if(check(i,Time[now][Rank[j]],id))break;
     }
       int End=i+Time[now][Rank[j]]-;
       for(i;i<=End;i++)work[id][i]=;
       Lasttime[now]=End;
       ans=max(ans,End);
     }
   cout<<ans<<endl;
   return ;
 }