Sum BZOJ 3944
Sum
【问题描述】
给定一个正整数 N ( N <= 231 - 1 )
求:
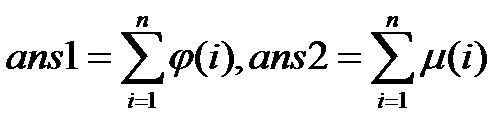
【输入格式】
【输出格式】
6
1
2
8
13
30
2333
【样例输出】
1 1
2 0
22 -2
58 -3
278 -3
1655470 2
题解:
首先推一波式子
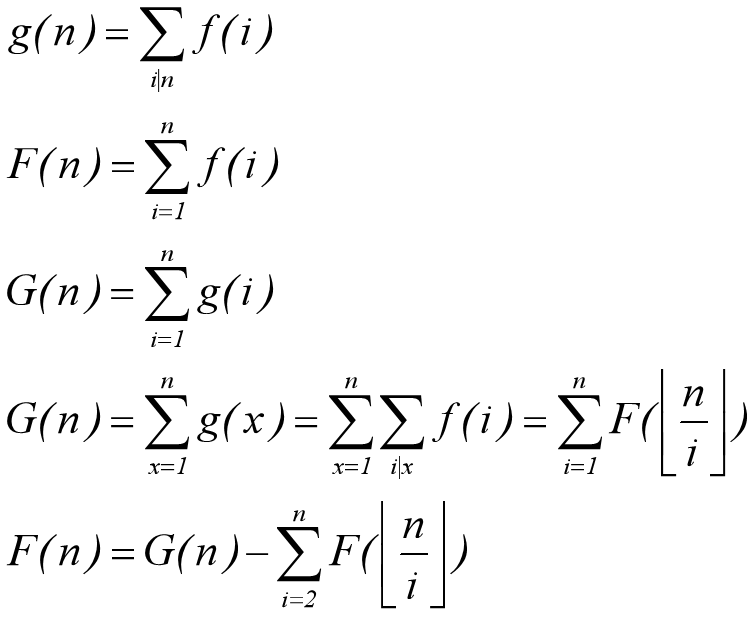
上式就是杜教筛的原理
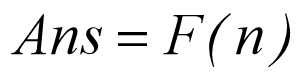
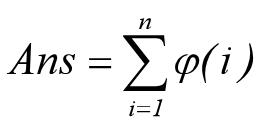 :
:
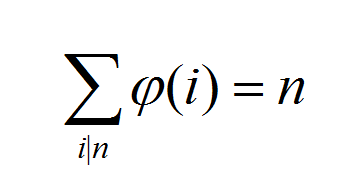
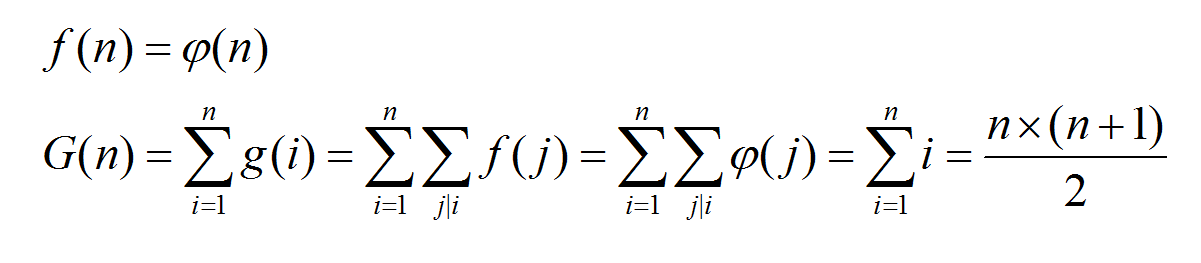
 :
:

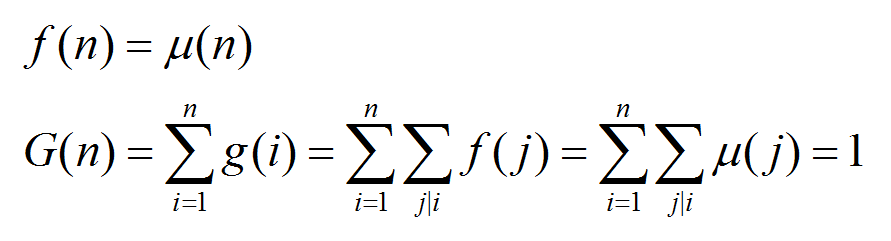
对于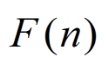 的求解方式在上面已经给出了
的求解方式在上面已经给出了
那么求出前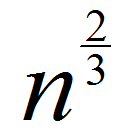 项答案并记忆化状态,就能达到
项答案并记忆化状态,就能达到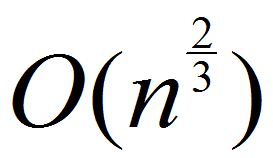 的时间复杂度
的时间复杂度
由于 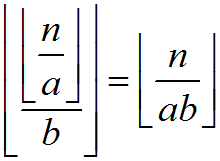 ,那么我们求的每一项的参数都是
,那么我们求的每一项的参数都是 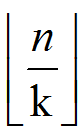 形式的
形式的
对于 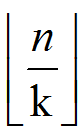 小于等于
小于等于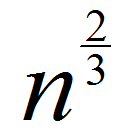 的答案我们已经预处理出了
的答案我们已经预处理出了
所以我们只需要记忆大于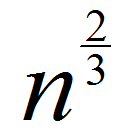 的答案
的答案
首先提出一个命题:对于  ,
,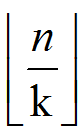 都不相同
都不相同
证明:
假设 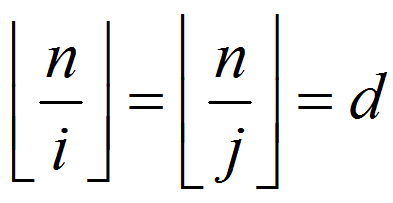 ,且
,且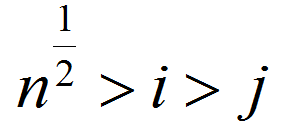
那么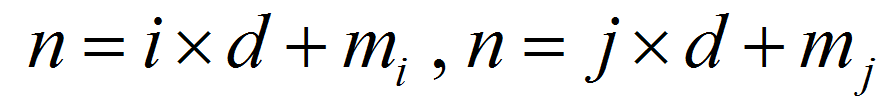
mi , mj 表示两者的余数,它们的差为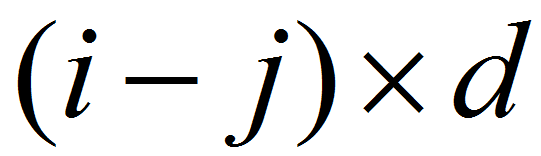
因为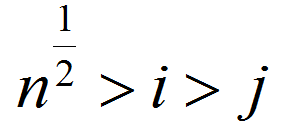 ,所以
,所以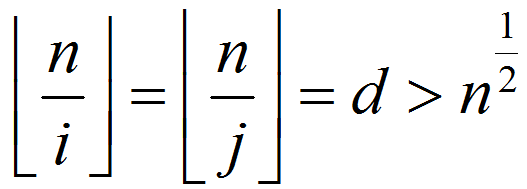
那么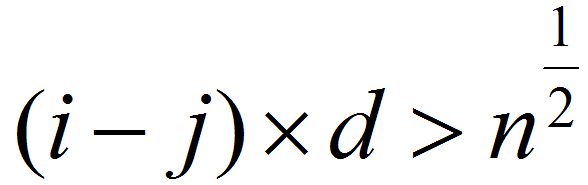 ,而
,而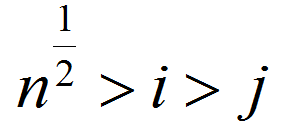 ,假设不成立
,假设不成立
所以不存在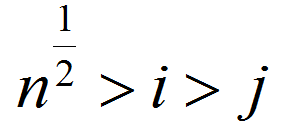 ,使得
,使得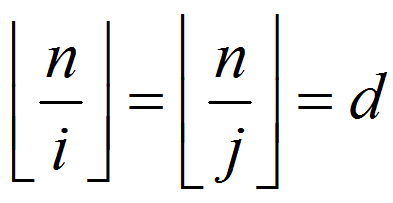
证毕
所以在  时,
时,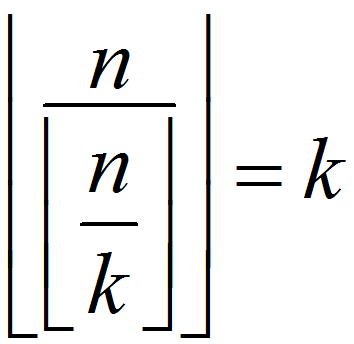 成立
成立
那么 ,我们就能直接使用数组存,对于每一个参数,我们将其除k的结果作为下标储存答案
,我们就能直接使用数组存,对于每一个参数,我们将其除k的结果作为下标储存答案
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxm = 2e6 + ;
const int maxn = 1e4 + ;
int n;
int pri[maxm];
bool vis[maxm];
struct couple
{
long long miu, phi;
};
couple ans[maxn], ori[maxm];
inline void Scan(int &x)
{
char c;
bool o = false;
while(!isdigit(c = getchar())) o = (c != '-') ? o : true;
x = c - '';
while(isdigit(c = getchar())) x = x * + c - '';
if(o) x = -x;
}
int m;
inline void Sieve()
{
int tot = ;
m = maxm - ;
ori[] = (couple) {, };
for(int i = ; i <= m; ++i)
{
if(!vis[i])
{
pri[++tot] = i;
ori[i] = (couple) {-, i - };
}
for(int j = ; j <= tot; ++j)
{
int k = pri[j];
long long s = (long long) i * k;
if(s > m) break;
vis[s] = true;
if(!(i % k))
{
ori[s].miu = ;
ori[s].phi = ori[i].phi * k;
break;
}
else
{
ori[s].miu = -ori[i].miu;
ori[s].phi = ori[i].phi * ori[k].phi;
}
}
}
for(int i = ; i <= m; ++i)
{
ori[i].miu += ori[i - ].miu;
ori[i].phi += ori[i - ].phi;
}
}
couple Solve(int x)
{
if(x <= m) return ori[x];
int e = n / x;
if(vis[e]) return ans[e];
int last;
couple c, s;
s.miu = , s.phi = x * ((long long) x + ) >> ;
for(long long i = ; i <= x; i = (long long) last + )
{
last = x / (x / i);
c = Solve(x / i);
s.miu -= c.miu * (long long) (last - i + ), s.phi -= c.phi * (long long) (last - i + );
}
vis[e] = true, ans[e] = s;
return s;
}
int main()
{
int T;
Scan(T);
Sieve();
while(T--)
{
Scan(n);
memset(vis, false, sizeof(vis));
if(n <= m) printf("%lld %lld\n", ori[n].phi, ori[n].miu);
else
{
couple answer = Solve(n);
printf("%lld %lld\n", answer.phi, answer.miu);
}
}
Sum BZOJ 3944的更多相关文章
- ●杜教筛入门(BZOJ 3944 Sum)
入门杜教筛啦. http://blog.csdn.net/skywalkert/article/details/50500009(好文!) 可以在$O(N^{\frac{2}{3}})或O(N^{\f ...
- BZOJ 3944: Sum [杜教筛]
3944: Sum 贴模板 总结见学习笔记(现在还没写23333) #include <iostream> #include <cstdio> #include <cst ...
- bzoj 3944: Sum(杜教筛)
3944: Sum Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 4930 Solved: 1313[Submit][Status][Discuss ...
- BZOJ 3944 Sum
题目链接:Sum 嗯--不要在意--我发这篇博客只是为了保存一下杜教筛的板子的-- 你说你不会杜教筛?有一篇博客写的很好,看完应该就会了-- 这道题就是杜教筛板子题,也没什么好讲的-- 下面贴代码(不 ...
- BZOJ.3944.Sum(Min_25筛)
BZOJ 洛谷 不得不再次吐槽洛谷数据好水(连\(n=0,2^{31}-1\)都没有). \(Description\) 给定\(n\),分别求\[\sum_{i=1}^n\varphi(i),\qu ...
- bzoj 3944 Sum —— 杜教筛
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=3944 杜教筛入门题! 看博客:https://www.cnblogs.com/zjp-sha ...
- BZOJ 3944 Sum 解题报告
我们考虑令: \[F_n = \sum_{d|n}\varphi(d)\] 那么,有: \[\sum_{i=1}^{n}F_i = \sum_{i=1}^{n}\sum_{d|i}\varphi(d) ...
- 【刷题】BZOJ 3944 Sum
Description Input 一共T+1行 第1行为数据组数T(T<=10) 第2~T+1行每行一个非负整数N,代表一组询问 Output 一共T行,每行两个用空格分隔的数ans1,ans ...
- 「bzoj 3944: Sum」
题目 杜教筛板子了 #include<iostream> #include<cstring> #include<cstdio> #include<cmath& ...
随机推荐
- bower使用
1,先安装nodejs(npm),Git 2,安装bower cmd执行到在项目文件夹下路径,执行npm install bower 3,执行bower init 项目根目录下将生成bower.js ...
- 远程连接 mySql数据库
远程连接 mySql数据库 一.安装并配置MySQL1.安装MySQL:运行mysql-essential-6.0.11-alpha-win32,按“MySQL+6.0+Windows下安装图解”完成 ...
- [BZOJ] 1441 Min
题意:给一堆数ai,求S=Σxiai,使得S最小且为正整数 根据裴蜀定理,一定存在ax+by=gcd(a,b),同理可以推广到n个整数 也就是说,在不考虑正负的情况下,所有数的gcd就是所求 #inc ...
- MHA
MHA 1. MHA简介 1.1 MHA工作原理总结为如下 1.2 MHA工具包介绍 2. 部署MHA 2.1 环境介绍 2.2 一主两从复制搭建 2.3 配置互信 2.4 下载MHA 2.5 安装M ...
- k8s调度的预选策略及优选函数
scheduler调度过程: Predicate(预选)-->Priority(优选)-->Select(选定)调度方式: 1.节点亲和性调度(NodeAffinity)使用n ...
- mysql的字符串连接符
以前用SQL Server 连接字符串是用“+”,现在数据库用mysql,写个累加两个字段值SQL语句居然不支持"+",郁闷了半天在网上查下,才知道mysql里的+是数字相加的操作 ...
- thinkphp5开发restful-api接口学习 教程视频 接口文档
目录 1. 获取验证码 2. 用户注册 3. 用户登录 4. 用户上传头像 5. 用户修改密码 6. 用户找回密码 7. 用户绑定手机号 8. 用户绑定邮箱 9. 用户绑定用户名(手机/邮箱) 10. ...
- 【原创】Mysql中事务ACID实现原理
引言 照例,我们先来一个场景~ 面试官:"知道事务的四大特性么?" 你:"懂,ACID嘛,原子性(Atomicity).一致性(Consistency).隔离性(Isol ...
- Hive学习笔记(四)-- hive的桶表
桶表抽样查询 查看hdfs上对应的文件内容 一个两个桶,第一个桶和第三个桶的数据 task = 4 4 / 2 = 2,一共是两个桶 第1个桶,第1+2个桶
- webdriver高级应用- 启动FireFox的同时打开Firebug
1. 首先本机Firefox浏览器需要安装一下firebug插件,具体怎么安装这里不赘述,网上教程很多. 2. 具体自动化实现的代码如下: #encoding=utf-8 from selenium ...
