斜率优化DP简单总结&&“土地购买”题解

今天刚刷完了斜率优化DP，简单从头回顾一下。

\[首先，能写出DP方程应该是最重要的，毕竟斜率只是用来优化的
\]

那么一个DP方程能用斜率优化，具备一种形式：

\[f[i]+s1[i]+A[i]*B[j]=f[j]+s2[j]
\]

其中，f[i]表示所求值，（s1[i]、A[i]）与（s2[j]、B[j]）分别表示只与i或j有关的一个表达式（可以是只有常数项）。

然后就可以建立一个横坐标为B[j]，斜率为A[i]，纵坐标为f[j]+s2[j]的函数。如果横坐标有单调性，那么只需单调队列保留一个凸壳或凹壳即可（任务安排2），否则就像需要支持任意插入、查询（任务安排3、4）。

基本形式大概就是上面那样，接下来从题中看点特别的。

1、任务安排系列

我们使用了费用提前计算思想。
通过前缀和使得整个式子只包含与i，j有关的变量和常数，通过移项，使得式子简化成f[i]+s1[i]+A[i]*B[j]=f[j]+s2[j]的形式，直接省去了j的枚举，时间复杂度降到O(N)。

2、运输小猫

通过每只小猫的游玩时间和位置信息，将其与饲养员出发时间建立联系，便与任务安排很像了。
同样使用前缀和将所有变量转为只与i，j有关的变量，最终式子化简为标准形式，时间O（N）。

3、特别行动队、仓库建设、玩具装箱

几乎没什么区别，将DP方程写出来之后，通过前缀和去化简变量，最终简化式子为标准形式即可。

从上面的这些题中可以看出，我们大量运用了前缀和，就是为了可以通过预处理将DP方程中的变量简化为只与i，j有关的量，以便将式子化为标准形式，$$所以斜率优化DP就是要去简化变量，转化式子，剩下的就可以斜率优化掉一层枚举了$$

4、但是前缀和并不万能，来看 “土地购买”

首先毫无头绪，没有像前几道题那样点明必须连续购买，而是想买多少卖多少，这朴素转移就很难，pu-tao↑。

但是为了比较好判断谁的l（长）比较大，先把他们按l sort一遍，得到一个a不严格递增的序列，由前几道题的做题经验想到应该取连续的一段，来证明一下：

反证：

如果不应该取连续的一段，那么就是取不连续的，num[i]表示i在序列中的位置，设num[a]<num[b]<num[c],取a，c，不取b。

如果取c不取b，说明w[c]（宽）<w[b],不然w[c]>w[b]&&l[c]>l[b]就必然会把b包括进来，接下来分类讨论一下：

w[a]<=w[b]:

显然b可以包括进a，不行。
w[a]>w[b]:

（1）：w[a]是b所包括范围之内最大的w

①：w[a]是c所包括范围之内最大的w，因为l[b]<=l[c],所以a属于b更优。

②：w[a]不是c所包括范围之内最大的w，那就可以把c所包括的最大的w[x]的x给b，因为l[b]<=l[c].

（2）：w[a]不是b所包括范围之内最大的w，那么a不会对b的答案造成影响，给b更优。

所以a应该跟b，即不连续的取一段不是最优解。

证毕

由上述证明过程引发出一个想法：$$ w[i]>w[j]\ and\ l[i]>l[j],j完全可以被i包含，j无用 $$,所以整个序列要去掉那些无用的元素，用以w为关键字单调递减队列跑一遍，即可得到最终序列，l递增，w递减：

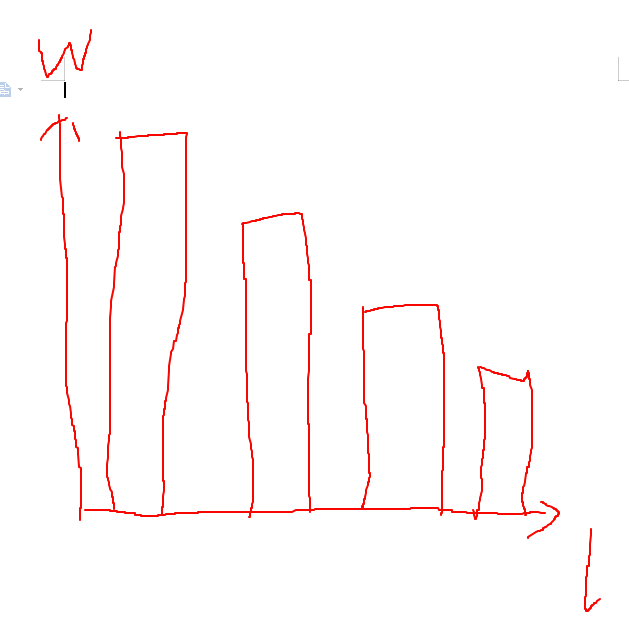
由此可以写出DP方程：$$f[i]=f[j]+l[i]*w[j+1]$$,完美符合标准形式，切横坐标-w[j+1]具有单调性，直接跑单调队列即可。

pu-tao↑zher↑↓

#include<bits/stdc++.h>

using namespace std;

#define fi first

#define se second

#define laoda MAN

#define MAN What Can I Say?

typedef long long ll;

typedef pair<int,int> pii;

const ll linf=0x3f3f3f3f7fffffff;

inline int read(){

	char c=getchar();int x=0;

	bool f=1;

	while(c<'0'||c>'9')f=c=='-'?0:1,c=getchar();

	while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();

	return f==0?-x:x;

}

const int N=5e4+10,inf=0x7f7f7f7f;

ll n,f[N],q[N],l=1,r,m[N];

struct jj{

	ll a,b;//a->l,b->w

	inline bool operator <(const jj &x)const{

		return a<x.a;

	}

}man[N];

int main(){

	#ifndef ONLINE_JUDGE

	freopen("in.in","r",stdin);

	freopen("out.out","w",stdout);

	#endif

	n=read();

	for(int i=1;i<=n;++i){

		man[i]={read(),read()};

	}

	sort(man+1,man+1+n);

	for(int i=1;i<=n;++i){

		while(l<=r&&man[q[r]].b<=man[i].b)--r;

		q[++r]=i;

	}

	for(int i=l;i<=r;++i)

		man[i-l+1]=man[q[i]];

	n=r-l+1;

	l=1,r=1;q[1]=0;

	for(int i=1;i<=n;++i){

		int j=q[l+1],k=q[l];

		while(l<r&&f[j]-f[k]<=man[i].a*(man[k+1].b-man[j+1].b))k=q[++l],j=q[l+1];

		f[i]=f[k]+man[i].a*man[k+1].b;

		j=q[r],k=q[r-1];

		while(l<r&&(f[j]-f[k])*(man[i+1].b-man[j+1].b)<=(f[i]-f[j])*(man[j+1].b-man[k+1].b))j=q[--r],k=q[r-1];

		q[++r]=i;

	}

	cout<<f[n];

}