多维数据处理之主成分分析(PCA)

在灵巧手与假手理论中，为了研究人手的运动协同关系，需要采集各个关节的运动学量或者多个采集点的肌电信号，然而由于人手关节数目或者EMG采集点数量较多，加上多次采样，导致需要过多的数据需要处理。然而事实上，这些数据存在相关性，换一种说法就是人手的某一运动被这些数据重复表达了，为了简化数据维度并尽可能的表征原始数据的特征，引入我们今天的主题-主成分分析(PCA)

 

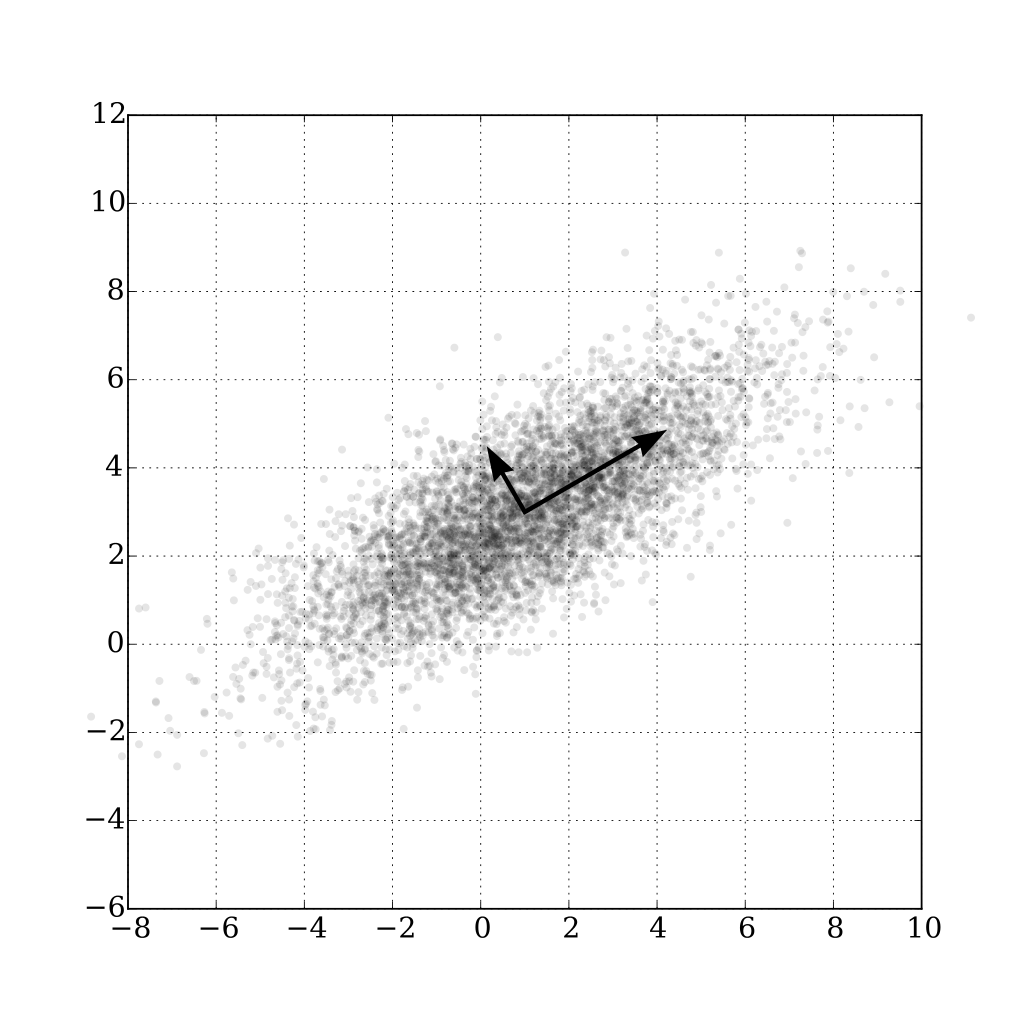
Ⅰ. 主成分分析(PCA)

主成分分析是一种处理过多维度数据的线性方法，该方法采用组合特征的方法来降维。从本质上来讲就是把高维的数据投影到低维空间中。这里又引出另一种线性分析方法-多重判别分析(MDA)，其与主成分分析均是在最小均方意义下的处理方法，区别在于前者目的是尽量区别开来各类数据，而主成分分析则是寻找最能代表原始数据的方法。

---

 Ⅱ. 推导

首先考虑将n个d维的样本(X₁,X_2,...Xn)投影到1维的情况。为了方便后面的推导，定义一个d维的向量X₀，为了使得X₀能够最好的代表这n个样本，我们用均方误差来衡量这个"最好"的程度，定义平方误差准则函数J₀(X₀)如下：

$$ J_0(X_0)=\sum_{k=1}^n||X_0-X_k||^2 \tag{1} $$

易证明得，X₀等于样本均值m时平方误差J₀(X₀)达到最小值，其中样本均值m为：

$$ m=\frac{1}{n}\sum_{k=1}^nX_k \tag{2} $$

证明如下：

$$ J_0(X_0)=\sum_{k=1}^n||(X_0-m)-(X_k-m)||^2=\sum_{k=1}^n||X_0-m||^2-2(X_0-m)^T\sum_{k=1}^n(X_k-m)+\sum_{k=1}^n||X_k-m||^2 \tag{3} $$

上式中第二项为0，第三项是与X₀无关的常数，故X₀等于m时，平方误差最小，得证。

得到样本均值后，样本均值可以理解为样本数据集的零维表达，为了得到能够表达全部数据的一维数据(一个数)，我们定义一个单位向量e，该向量位于一条通过样本均值点的直线上，其它数据点X₁,X_2,...Xn可以表示为：

$$ X=m+ae \tag{4} $$

上式(4)中，a为向量对应与基于基底e的系数，被成为主成分(principal component)，由此，对于每一个原本为d维的样本点，在确定了样本均值m和基底e后，我们都可以用一个一维的数据a表示我们新的样本点，如X_k对应于m+a_ke，要注意的是两者并不相等，后文中我们会通过确定一个最优的基底e使得两者的距离和最小。经过以上步骤，我们就把n个d维的样本点X₁,X_2,...Xn降维成了n个1维的数据a₁,a₂,...a_n,这本质上就是重新确定了一个数量更小的坐标轴来确定空间上的点，a表示每个数据点在该基底上的投影大小，只不过我们这个例子只有一个基底，即d维降维成1维。

我们需要确定最优的a_k和基底e的方向使得式(5)中平方误差准则函数最小，注意到这是关于a_k(k=1,2...n)和基底e的函数：

$$ J_1(a_1,a_2,...a_n,e)=\sum_{k=1}^n||(m+a_ke)-X_k||^2=\sum_{k=1}^n(a_k^2||e||^2-2a_ke^T(X_k-m))+\sum_{k=1}^n||X_k-m||^2 \tag{5} $$

首先关于式(5)对a_k求偏导，并令结果为0，得到：

$$ \frac{\partial J_1}{\partial a_k}=2a_k||e||^2-2e^T(X_k-m)=0 \tag{6} $$

由式(6)可得最优的ak为：

$$ a_k=\frac{e^T(X_k-m)}{||e||^2}=e^T(X_k-m) \tag{7} $$

几何上的意义为a_k可由向量(X_k-m)向通过样本均值的直线e做垂直投影得到。在得到a_k后，我们再来考虑如何选择基底e使得平方误差准则函数最小，同理，我们关于式(5)对e求偏导令结果为0即可，不过在此之前需要对式(5)做一些处理，将a_k式(7)代入式(5)中得到：

$$ J_1(e)=-\sum_{k=1}^ne^T(X_k-m)(X_k-m)^Te+\sum_{k=1}^n||X_k-m||^2=-e^TSe+\sum_{k=1}^n||X_k-m||^2 \tag{8} $$

上式中称S为离散度矩阵或者散布矩阵，其形式为：

$$ S=\sum_{k=1}^n(X_k-m)(X_k-m)^T \tag{9} $$

由式(8)显然我们可以得出，为使得J₁(e)最小，需要使e^_TSe最大，我们这里使用拉格朗日乘子法来最大化e^_TSe，约束条件为等式||e||=1，用λ来表示拉格朗日乘子有：

$$ u=e^TSe-\lambda(e^Te-1) \tag{10} $$

对式(10)对e求偏导并令其为0我们可以得到：

$$ Se=\lambda e \tag{11} $$

由式(11)我们可以很明显的看到，e的解为离散度矩阵的特征向量，λ为与之对应的特征值，同时可以得出e^TSe=e^Tλe=λe^Te=λ，由此，为了最大化e^TSe，只需找出该离散度矩阵S的最大的特征值，再得出相应的特征向量作为基底e即可。

至此，d维降1维的问题已经得到解决，我们再把问题扩展到d维降d'维的问题，即求解下式(12)中的a和e:

$$ X=m+\sum_{i=1}^{d'}a_ie_i \tag{12} $$

这里不再给出证明，结论如下：最优的基底e₁,e₂,...e_d'分别为离散度矩阵S对应的d'个最大特征值所对应的特征向量，另外由于离散度矩阵S为实对称矩阵，所以各个基底互相正交，而主成分a_ki同理可以得出是样本向量在各个基底上的垂直投影。

---

 Ⅲ. 计算步骤总结

我们可以对比看一看维基百科上关于计算PCA的步骤，如下图，与我上文中说到的步骤不同之处在于wikipedia上的方法计算的是协方差矩阵，如果仔细算一算就会发现上文中讲到的离散度矩阵或者散布矩阵事实上是该协方差矩阵的(n-1)倍。其它步骤原理是一致的：