BST,AVL,B,B+,B*,红黑树

BST(右)和AVL(左)

比较：AVL树每个结点的左右子树的深度差的绝对值不大于1

B - tree

特点：所有结点都包含数据信息，不同查询的效率不同，特殊的：二阶B树就是AVL，三阶B树就是2-3树

B+ - tree

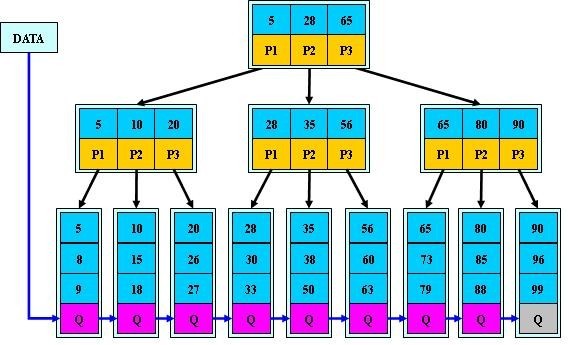
特点：B - tree的变种，只有叶子结点才包含数据信息，所有的叶子结点有指针连接起来，所有查询路径均为：从根结点到叶子结点。范围查询效率比较高，因此常用数据库索引

B* - tree

特点：B+树的变种，除了叶子结点直接有指针连接起来，非根结点非叶子结点也用指针将每层的结点连接了起来
改进：与B+树分裂相比，可以将边缘结点移到兄弟结点，然后更新兄弟结点对应父结点键值，最后将新值插入，在这个过程中不需要新建结点。

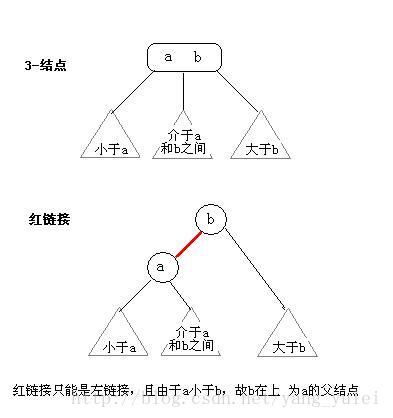
红黑树

特点：用红链接表示3分叉结点的2-3树，每个结点内部多了个color域，color的取值取决于指向它的线条的颜色，如果为红色，color=true，如果为黑色，color=false
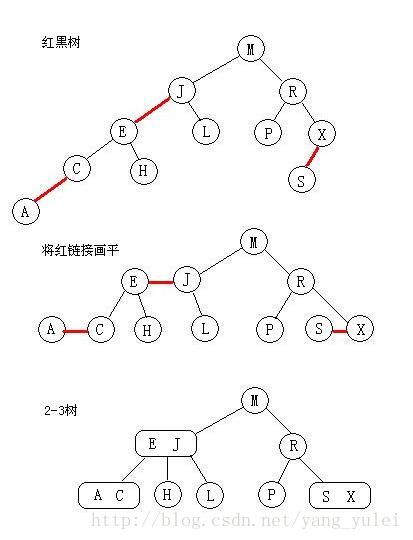
替换本质如下；

替换演示：

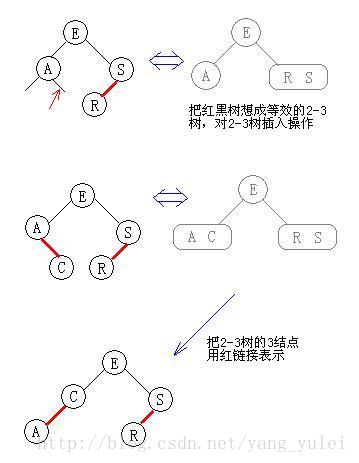
插入演示：

参考：http://blog.csdn.net/yang_yulei/article/details/26066409