最小可观(Minimal Observability Problem in Conjunctive Boolean Networks)
1. 什么是 conjunctive Boolean network (CBN)
仅仅包含and运算。
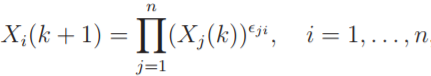
下面这个式子为恒定更新函数
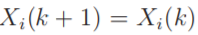
2. 什么是可观
定义在时刻k是CBN的状态为 X(k) := [X1(k) . . . Xn(k) ]′ 以及输出为Y(k) :=[Y1(k) . . . Ym(k) ]′ .
a). CBN在离散时间{0, 1, . . . , N}上可观,如果对于任意两个不同的初始状态X(0)和X'(0)产生不同的输出{Y(0),...,Y(N)}和{Y’(0),...,Y’(N)}。
b). CBN可观,如果存在N,使得a)成立。
3. 可观必须具有的性质(等价条件)
a) 性质O1:对于每一个非直接可观的节点Xi,Xi是某一个节点Xj唯一的入边的节点,即,存在一个节点Xj,使得,Nin(Xj)=Xi。
b) 性质O2:对于每一个仅由非直接可观的节点组成的环C。C包含一个节点Xi,Xi是某一个节点Xj唯一的入边的节点,即,存在一个节点Xj,使得,Nin(Xj)=Xi并且Xj在环C的外部。
4. 例子
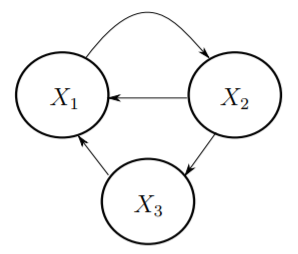
Ex 1. 添加观测器,Y1(k)=X1(K)。则给定输出Y1(0),Y1(1),就可以推出初始状态分别为X1(0)=Y1(0),X2(0)=Y1(1)。
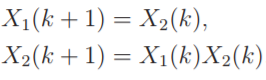
Ex 2. CBN不具有性质O1,非可观节点X3,不存在任何一个节点,使得性质O1成立。[0 0 0]'和[0 0 1]'是无法区分的,因为它们的输出Y1(k)=0对于所有的k≥0。
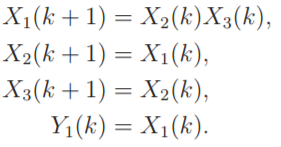
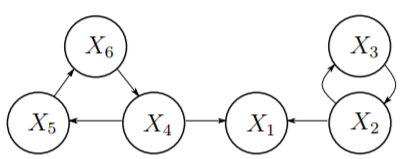
Ex 3. CBN满足性质O1,但是不满足性质O2。对于由X4,X5,X6构成的环,X4不是X1唯一的进入的节点。[0 0 0 0 0 0]‘和[0 0 0 1 1 1]'对应的输出Y1(k)=0对于所有的k≥0。
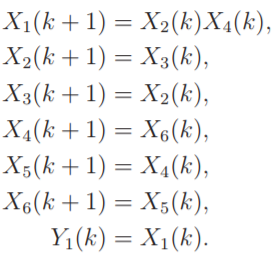
最小可观(Minimal Observability Problem in Conjunctive Boolean Networks)的更多相关文章
- (KMP 最大表示最小表示)String Problem -- hdu-- 3374
http://acm.hdu.edu.cn/showproblem.php?pid=3374 String Problem Time Limit: 2000/1000 MS (Java/Others) ...
- NCPC 2015 - Problem A - Adjoin the Networks
题目链接 : http://codeforces.com/gym/100781/attachments 题意 : 有n个编号为0-n-1的点, 给出目前已经有的边(最多n-1条), 问如何添加最少的边 ...
- HDU 3374 String Problem (KMP+最大最小表示)
HDU 3374 String Problem (KMP+最大最小表示) String Problem Time Limit: 2000/1000 MS (Java/Others) Memory ...
- VirtualBox上安装CentOS-7(Minimal)
Windows 10家庭中文版,VirtualBox 5.2.12,CentOS 7(Minimal版), 因为听到大家在谈论CentOS,阿里云上也有CentOS,CentOS还是Red Hat出品 ...
- List of NP-complete problems
This is a list of some of the more commonly known problems that are NP-complete when expressed as de ...
- hadoop作业调优参数整理及原理(转)
1 Map side tuning参数 1.1 MapTask运行内部原理 当map task开始运算,并产生中间数据时,其产生的中间结果并非直接就简单的写入磁盘.这中间的过程比较复杂,并且利用到了内 ...
- hadoop作业调优参数整理及原理【转】
1 Map side tuning参数 1.1 MapTask运行内部原理 当map task开始运算,并产生中间数据时,其产生的中间结果并非直接就简单的写入磁盘.这中间的过程比较复杂,并且利用到了内 ...
- 代码世界中的Lambda
“ λ ”像一个双手插兜儿,独自行走的人,有“失意.无奈.孤独”的感觉.λ 读作Lambda,是物理上的波长符号,放射学的衰变常数,线性代数中的特征值……在程序和代码的世界里,它代表了函数表达式,系统 ...
- Maximum Flow and Minimum Cut
最大流最小割 Introduction Mincut Problem 最小割问题,输入是带权有向图,有一个源点 s(source)和一个汇点 t(target),边的权重在这里称作容量(capacit ...
随机推荐
- 十九、RF接口测试汇总(一)
搭建项目:转自 http://chuansong.me/n/1858477 A.请求方式为get请求 方式一:导入RequestsLibrary库,get request [ alias | ...
- 4、Shiro之IniRealm以及用户登录认证,角色认证,权限认证
1.我们在项目test文件夹下面新建resourse文件夹并将她设置为资源文件夹: 2.在resourse文件夹下面新建user.ini文件 user.ini文件里面声明一个用户: 先写一个用户标签[ ...
- 数据科学家人才危机现象,是FOMO还是Silver?
数据科学家人才危机现象,是FOMO还是Silver? 数据科学家的人才短缺和薪水高涨已经达到了顶板,未来还会持续下去吗? 在过去几年中,高级分析(#大数据#分析)空间一直经历着严重的FOMO(害怕错过 ...
- C# 获取当前网页HTML
//引用COM组件 //Microsoft HTML Object Library //Microsoft Internet Controls SHDocVw.ShellWindows shellWi ...
- hibernate 2 多对多映射
一.实体类 1.Classes.java package cn.gs.wwg.entity; import java.util.Set; public class Classes { private ...
- 【Qt开发】【VS开发】【Linux开发】OpenCV、Qt-MinGw、Qt-msvc、VS2010、VS2015、Ubuntu Linux、ARM Linux中几个特别容易混淆的内容
[Qt开发][VS开发][Linux开发]OpenCV.Qt-MinGw.Qt-msvc.VS2010.VS2015.Ubuntu Linux.ARM Linux中几个特别容易混淆的内容 标签:[Qt ...
- 1~n的全排列--阅文集团2018校招笔试题
题目大意:给定整数n,求出1~n的全排列 示例 输入:n=3 输出:[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1] import java.util.S ...
- Maximum Depth of Binary Tree(二叉树最大深度)
来源:https://leetcode.com/problems/maximum-depth-of-binary-tree Given a binary tree, find its maximum ...
- Spring对Jdbc的封装——JdbcTemplate的使用
链接:https://pan.baidu.com/s/15luDElW4oeEaP0nvEQ_40w 提取码:i2r1 JdbcTemplate是Spring对JDBC的封装,目的是使JDBC更加易于 ...
- Windows netcat 的工具的简单使用
1. 下载 https://eternallybored.org/misc/netcat/ 2. 将目录添加到环境变量 C:\Work\netcat 3. 简单实验 4. 查看说明 UPDATE // ...
